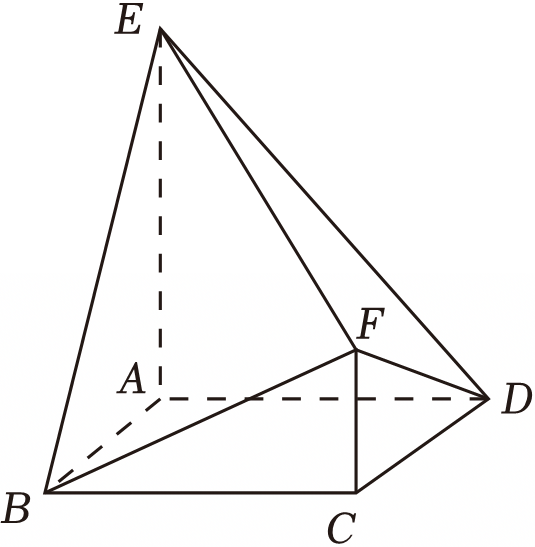
如图．在多面体$ABCDEF$中，平面$EAB\perp$平面$ABCD$，平面$EAD\perp$平面$ABCD$，$ABCD$是菱形，$\angle ABC=60^\circ$，$AB=2$，$FC//EA$，$EA=3$，$FC=1$．

$(1)$证明：$FC\perp$平面$ABCD$；

$(2)$求二面角$B-EF-D$的平面角的余弦值．

$(1)$证明见解析；

$(2)$$-\\dfrac{1}{5}$

$(1)$在平面$ABE$中，作$EM\perp AB$，在平面$EAD$中，作$EN\perp AB$，

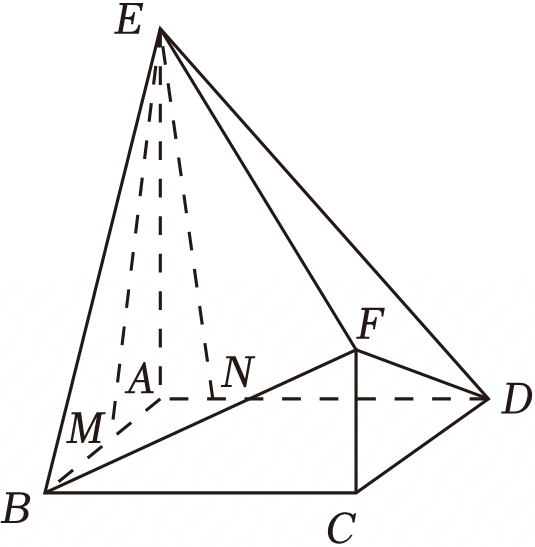
$\because $ 平面$EAB\perp$平面$ABCD$，平面$EAD\perp$平面$ABCD$

$\therefore EM\perp$平面$ABCD$，$EN\perp$平面$ABCD$，

则$EM$，$EN$重合，即$EM$，$EN$是平面$EAB$与平面$EAD$的公共交线，

即$EM$，$EN$与$EA$重合，即$EA\perp$平面$ABCD$，

$\because FC//EA$，

$\therefore FC\perp$平面$ABCD$．

$(2)$$\because ABCD$是菱形，$\angle ABC=60^\circ$，$AB=2$，$EA=3$，$FC=1$．

$\therefore $ 设$AC$，$BD$的交点是$O$，

则$AC=AB=BC=2$，$AO=OC=1$，$OB=OD=\sqrt{3}$，

以$O$为坐标原点，建立空间直角坐标系如图：

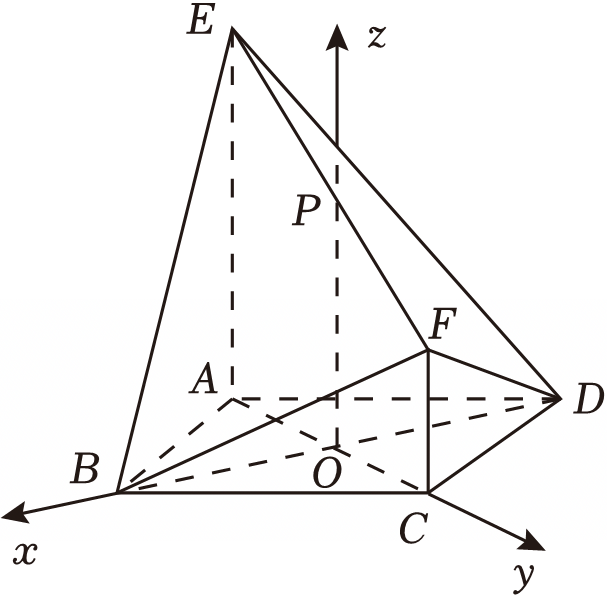
则$B(\sqrt{3},0,0)$，$E(0,-1,3)$，$F(0,1,1)$，$D(-\sqrt{3},0,0)$，

则$\overrightarrow{EF}=(0,2,-2)$，$\overrightarrow{BF}=(-\sqrt{3},1,1)$，$\overrightarrow{DF}=(\sqrt{3},1,1)$，

设平面$BEF$的法向量为$\boldsymbol{m}=(x,y,z)$，平面$DEF$的法向量为$\boldsymbol{n}=(a,b,c)$，

由$\begin{cases}{\boldsymbol{m}\cdot \overrightarrow{EF}=0}\\ {\boldsymbol{m}\cdot \overrightarrow{BF}=0}\end{cases}$得$\begin{cases}{-\sqrt{3}x+y+z=0}\\ {2y-2z=0}\end{cases}$，

令$y=\sqrt{3}$，则$z=\sqrt{3}$，$x=2$，即$\boldsymbol{m}=(2,\sqrt{3},\sqrt{3})$，

由$\begin{cases}{\boldsymbol{n}\cdot \overrightarrow{EF}=0}\\ {\boldsymbol{n}\cdot \overrightarrow{DF}=0}\end{cases}$，得$\begin{cases}{2b-2c=0}\\ {\sqrt{3}a+b+c=0}\end{cases}$，

令$b=\sqrt{3}$，则$c=\sqrt{3}$，$a=-2$，即$\boldsymbol{n}=(-2,\sqrt{3},\sqrt{3})$，

则$\cos\langle \boldsymbol{m},\boldsymbol{n}\rangle=\dfrac{\boldsymbol{m}\cdot \boldsymbol{n}}{\vert \boldsymbol{m}\vert \vert \boldsymbol{n}\vert }=\dfrac{-4+3+3}{\sqrt{10}\times \sqrt{10}}=\dfrac{2}{10}=\dfrac{1}{5}$．

由图象知二面角$B-EF-D$是钝二面角，

则二面角的余弦值为$-\dfrac{1}{5}$．