在棱长为$2$的正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$E$为棱$BC$的中点，点$P$在正方体的表面上运动，且满足$B_{1}P\perp D_{1}E$，则点$P$的运动轨迹的周长是                  ．

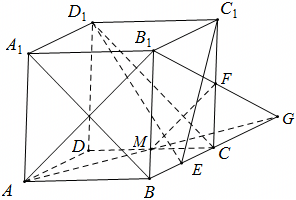
如图，取$CC_{1}$的中点$F$，连接$B_{1}F$并延长，交直线$BC$于点$G$，

连接$AG$，交$CD$于点$M$，连接$AB_{1}$，$A_{1}B$，$CD_{1}$，$FM$，$C_{1}E$，

$\because $ 在正方形$BCC_{1}B_{1}$中，$E$，$F$分别为$BC$，$CC_{1}$中点，

$\therefore B_{1}F\perp C_{1}E$，

又$\because D_{1}C_{1}\perp$平面$BCC_{1}B_{1}$，$B_{1}F\subset$平面$BCC_{1}B_{1}$，

$\therefore D_{1}C_{1}\perp B_{1}F$，

$\because D_{1}C_{1}$与$C_{1}E$是平面$D_{1}C_{1}E$内的相交直线，

$\therefore B_{1}F\perp$平面$D_{1}C_{1}E$，可得$B_{1}F\perp D_{1}E$．

又$\because $ 正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$AB_{1}\perp$平面$A_{1}D_{1}CB$，$D_{1}E\subset$平面$A_{1}D_{1}CB$，

$\therefore AB_{1}\perp D_{1}E$，

结合$B_{1}F$、$AB_{1}$是平面$D_{1}C_{1}E$内的相交直线，可得$D_{1}E\perp$平面$AB_{1}G$，

$\because $ 四边形$AB_{1}FM$是平面$AB_{1}G$与正方体相交所得截面，

$\therefore $ 点$P$的运动轨迹是四边形$AB_{1}FM$．

$\rm Rt$$\triangle $$CMF$中，$MF=\sqrt{CM^{2}+CF^{2}}=\sqrt{2}$；$\rm Rt$$\triangle $$ADM$中，$AM=\sqrt{AD^{2}+DM^{2}}=\sqrt{5}$；

$\rm Rt$$\triangle $$B_{1}C_{1}F$中，$B_{1}F=\sqrt{{B}_{1}{\rm {C}}_{1}^{2}+{C}_{1}F^{2}}=\sqrt{5}$．

结合$AB_{1}=2\sqrt{2}$，可得四边形$AB_{1}FM$的周长为$2\sqrt{5}+3\sqrt{2}$，

即点$P$的运动轨迹的周长是$3\sqrt{2}+2\sqrt{5}$．

故答案为：$3\sqrt{2}+2\sqrt{5}$