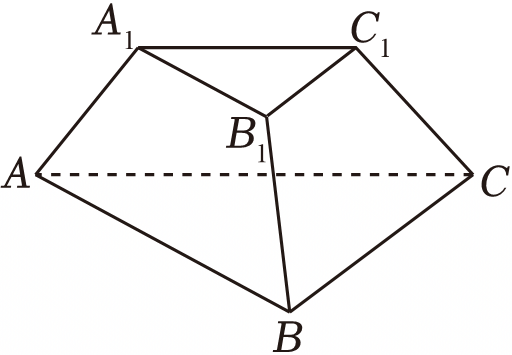
如图，已知三棱台$ABC-A_{1}B_{1}C_{1}$的体积为$\dfrac{14\sqrt{3}}{3}$，底面$\triangle $$ABC$是以$B$为直角顶点的等腰直角三角形，平面$ABB_{1}A_{1}\perp$平面$ABC$，且$AA_{1}=A_{1}B_{1}=BB_{1}=\dfrac{1}{2}AB$．

$(1)$证明：$BC\perp$平面$ABB_{1}A_{1}$；

$(2)$求点$B$到平面$ACC_{1}A_{1}$的距离；

$(3)$在线段$CC_{1}$上是否存在点$F$，使得二面角$F-AB-C$的大小为$\dfrac{\pi }{6}$？若存在，求出$CF$的长；若不存在，请说明理由．

$(1)$证明见解析；

$(2)$$\\dfrac{4\\sqrt{21}}{7}$；

$(3)$存在，$CF=\\dfrac{8\\sqrt{2}}{5}$

$(1)$在三棱台$ABC-A_{1}B_{1}C_{1}$中，平面$ABB_{1}A_{1}\perp$平面$ABC$，$AB\perp BC$，

而平面$ABB_{1}A_{1}\cap$平面$ABC=AB$，$BC\subset$平面$ABC$，

$\therefore BC\perp$平面$ABB_{1}A_{1}$．

$(2)$由棱台性质知：延长$AA_{1}$，$BB_{1}$，$CC_{1}$交于一点$P$，

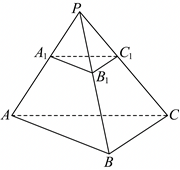
由${A}_{1}{B}_{1}=\dfrac{1}{2}AB$，得${S}_{\triangle ABC}=4{S}_{\triangle {A_1}{B}_{1}{C}_{1}}$，

点$P$到平面$ABC$的距离为到平面$A_{1}B_{1}C_{1}$距离的$2$倍，则${V}_{P-ABC}=8{V}_{P-{A_1}{B}_{1}{C}_{1}}$，

于是${V}_{P-ABC}=\dfrac{8}{7}{V}_{ABC-{A_1}{B}_{1}{C}_{1}}=\dfrac{8}{7}\times \dfrac{14\sqrt{3}}{3}=\dfrac{16\sqrt{3}}{3}$，

由$BC\perp$平面$ABB_{1}A_{1}$，得$BC$为点$C$到平面$PAB$的距离，

又$A_{1}B_{1}//AB$，则$A_{1}$是$PA$的中点，$PA_{1}=AA_{1}=A_{1}B_{1}=PB_{1}$，

即$\triangle $$PA_{1}B_{1}$为正三角形，$\triangle $$PAB$为正三角形，

设$AB=2x$，则$BC=PA=PB=AB=2x$，

${V}_{P-ABC}=\dfrac{1}{3}{S}_{\triangle PAB}\cdot BC=\dfrac{1}{3}\times \dfrac{\sqrt{3}}{4}\times (2x)^{2}\times 2x=\dfrac{2\sqrt{3}}{3}{x}^{3}=\dfrac{16\sqrt{3}}{3}$，解得$x=2$，

$AB=BC=PA=PB=4$，由$PB\subset$平面$PAB$，得$BC\perp PB$，$AC=PC=4\sqrt{2}$，

${S}_{\triangle PAC}=\dfrac{1}{2}\times 4\times \sqrt{(4\sqrt{2})^{2}-{2}^{2}}=4\sqrt{7}$，

设点$B$到平面$ACC_{1}A_{1}$的距离为$d$，

由$V_{P-ABC}=V_{B-PAC}$，得$\dfrac{1}{3}{S}_{\triangle PAC}\cdot d=\dfrac{4\sqrt{7}}{3}d=\dfrac{16\sqrt{3}}{3}$，

解得：$d=\dfrac{4\sqrt{21}}{7}$．

即点$B$到平面$ACC_{1}A_{1}$的距离为$\dfrac{4\sqrt{21}}{7}$．

$(3)$由$BC\perp$平面$ABB_{1}A_{1}$，$BC\subset$平面$ABC$，得平面$ABC\perp$平面$PAB$，取$AB$中点$N$，连接$PN$，

在正$\triangle $$PAB$中，$PN\perp AB$，而平面$ABC\cap$平面$PAB=AB$，则$PN\perp$平面$ABC$，而$CN\subset$平面$ABC$，

则$PN\perp CN$，又$PN\subset$平面$PNC$，则平面$PNC\perp$平面$ABC$，作$FE\perp CN$于$E$，

平面$PNC\cap$平面$ABC=CN$，则$FE\perp$平面$ABC$，$FE//PN$，而$AB\subset$平面$ABC$，则$AB\perp FE$，

作$ED\perp AB$于$D$，连接$FD$，$DE\cap FE=E$，$DE$，$FE\subset$平面$DEF$，则$AB\perp$平面$DEF$，

而$FD\subset$平面$DEF$，于是$AB\perp FD$，$\angle FDE$即二面角$F-AB-C$的平面角，

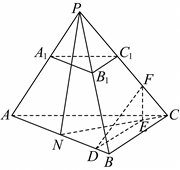
设$FE=\sqrt{3}t$，由$(2)$知：$PN=2\sqrt{3}$，$CN=\sqrt{B{C}^{2}+B{N}^{2}}=2\sqrt{5}$，

由$\dfrac{EF}{PN}=\dfrac{CE}{CN}$，得$CE=\dfrac{\sqrt{5}}{\sqrt{3}}\cdot \sqrt{3}t=\sqrt{5}t$，$EN=2\sqrt{5}-\sqrt{5}t$，

由$DE//BC$，得$DE=\dfrac{EN}{CN}\cdot BC=\dfrac{2\sqrt{5}-\sqrt{5}t}{2\sqrt{5}}\times 4=4-2t$，

若存在$F$使得二面角$F-AB-C$的大小为$\dfrac{\pi }{6}$，

则$\tan \angle FDE=\tan \dfrac{\pi }{6}=\dfrac{FE}{DE}=\dfrac{\sqrt{3}t}{4-2t}=\dfrac{\sqrt{3}}{3}$，解得$t=\dfrac{4}{5}$，

$CF=\sqrt{C{E}^{2}+E{F}^{2}}=2\sqrt{2}t=\dfrac{8\sqrt{2}}{5}\lt C{C}_{1}=2\sqrt{2}$，

$\therefore $ 存在满足题意的点$F$，$CF=\dfrac{8\sqrt{2}}{5}$．