如图，在三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，$AB\perp AC$，$AB=AC$，$A{{A}_{1}}=2AB$，点${{A}_{1}}$在底面$ABC$的射影为$BC$的中点$O$，点$M$为$B_{1}C_{1}$的中点$.$

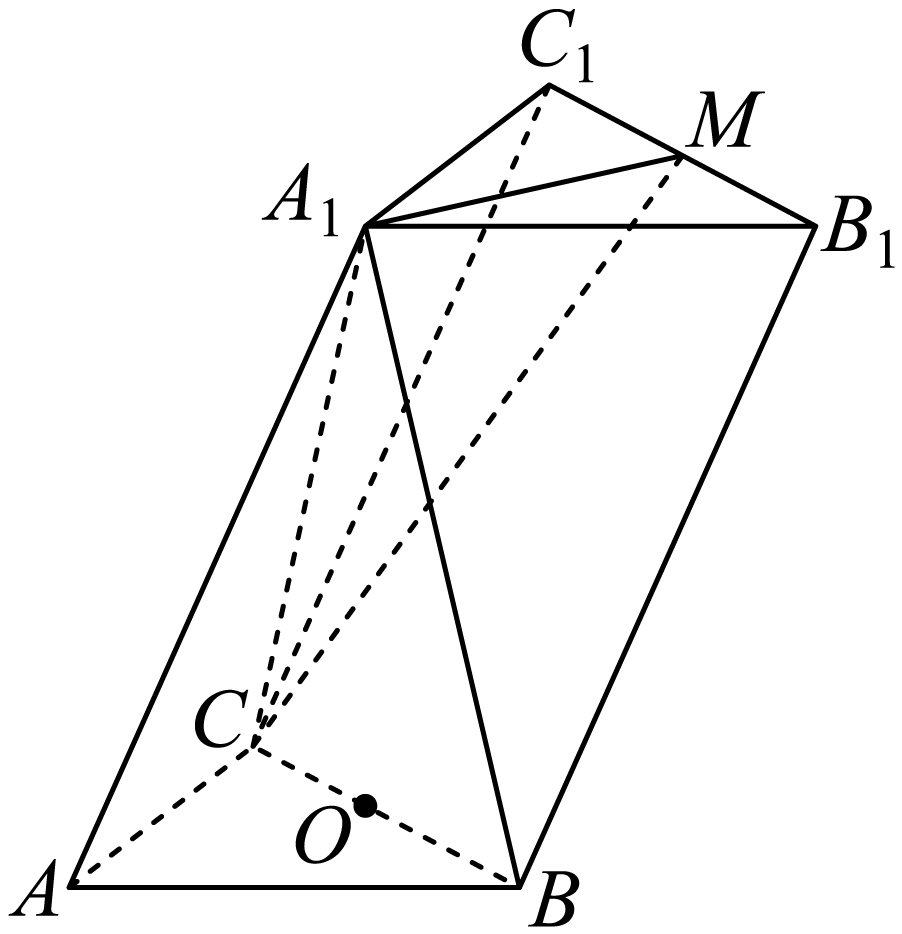
$(1)$求证：${{A}_{1}}M\perp $平面${{A}_{1}}BC$；

$(2)$求异面直线${{A}_{1}}O$和$B_{1}C_{1}$夹角的大小；

$(3)$设点$P$为底面$ABC$内（包括边界）的动点，且${{B}_{1}}P//$平面${{A}_{1}}MC$，若点$P$的轨迹长度为$\sqrt{2}$，求三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$的侧面积$.$

$(1)$证明见解析；

$(2)$${{90}^{^\\circ }}$；

$(3)$$8\\sqrt{2}+4\\sqrt{15}$

$(1)$在三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，连接$AO,MO,{{A}_{1}}O$，

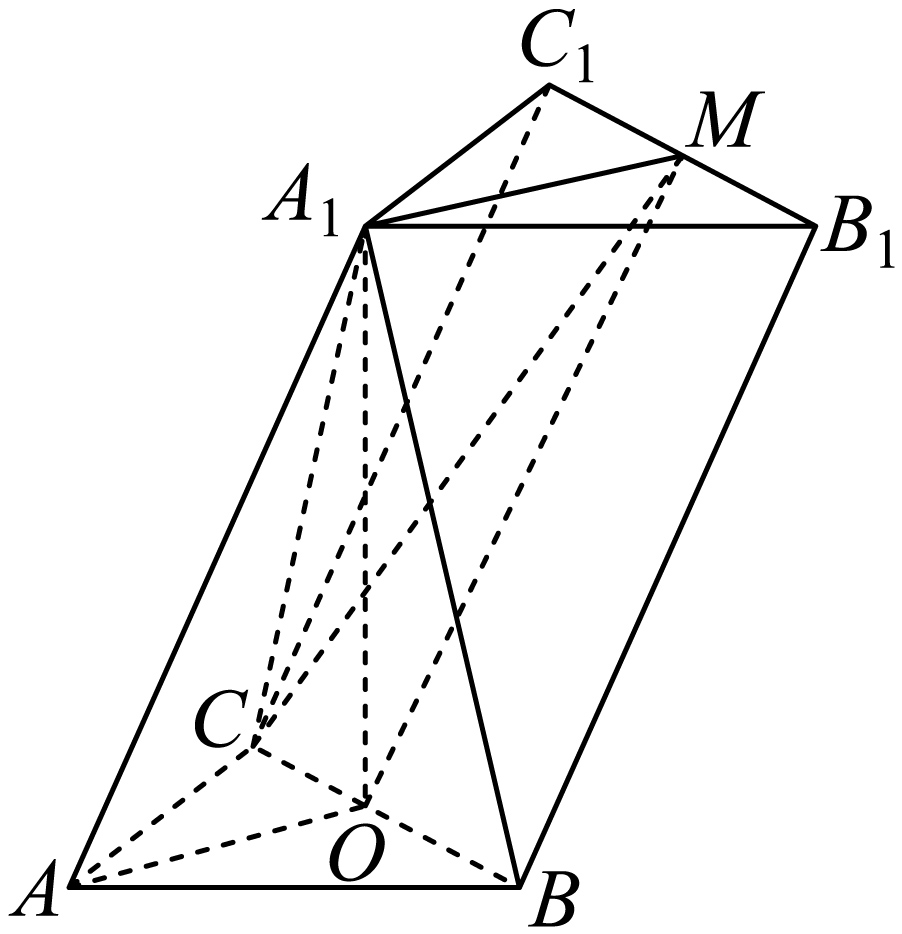
由$AB=AC$，$O$为$BC$的中点，得$AO\perp BC$，

又${{A}_{1}}O\perp $平面$ABC$，且$AO,BC\subset $平面$ABC$，则$AO\perp {{A}_{1}}O$，$BC\perp {{A}_{1}}O$，

由$BC\cap {{A}_{1}}O=A$，$BC,{{A}_{1}}O\subset $平面${{A}_{1}}BC$，得$AO\perp $平面${{A}_{1}}BC$，

在$BC{{C}_{1}}{{B}_{1}}$中，$O,M$分别为$BC,{{B}_{1}}{{C}_{1}}$的中点，则$OM//C{{C}_{1}}$，$OM=C{{C}_{1}}$，

而$A{{A}_{1}}//C{{C}_{1}}$，$A{{A}_{1}}=C{{C}_{1}}$，则$OM//A{{A}_{1}}$，$OM=A{{A}_{1}}$，

即四边形$AOM{{A}_{1}}$为平行四边形，则${{A}_{1}}M//AO$，

$\therefore {{A}_{1}}M\perp $平面${{A}_{1}}BC$$.$

$(2)$在三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，${{B}_{1}}{{C}_{1}}//BC$，

由$(1)$知，$BC\perp {{A}_{1}}O$，则${{B}_{1}}{{C}_{1}}\perp {{A}_{1}}O$，

$\therefore $ 异面直线${{A}_{1}}O$和$B_{1}C_{1}$夹角的大小为${{90}^{^\circ }}$$.$

$(3)$连接$A{{B}_{1}},O{{B}_{1}}$，

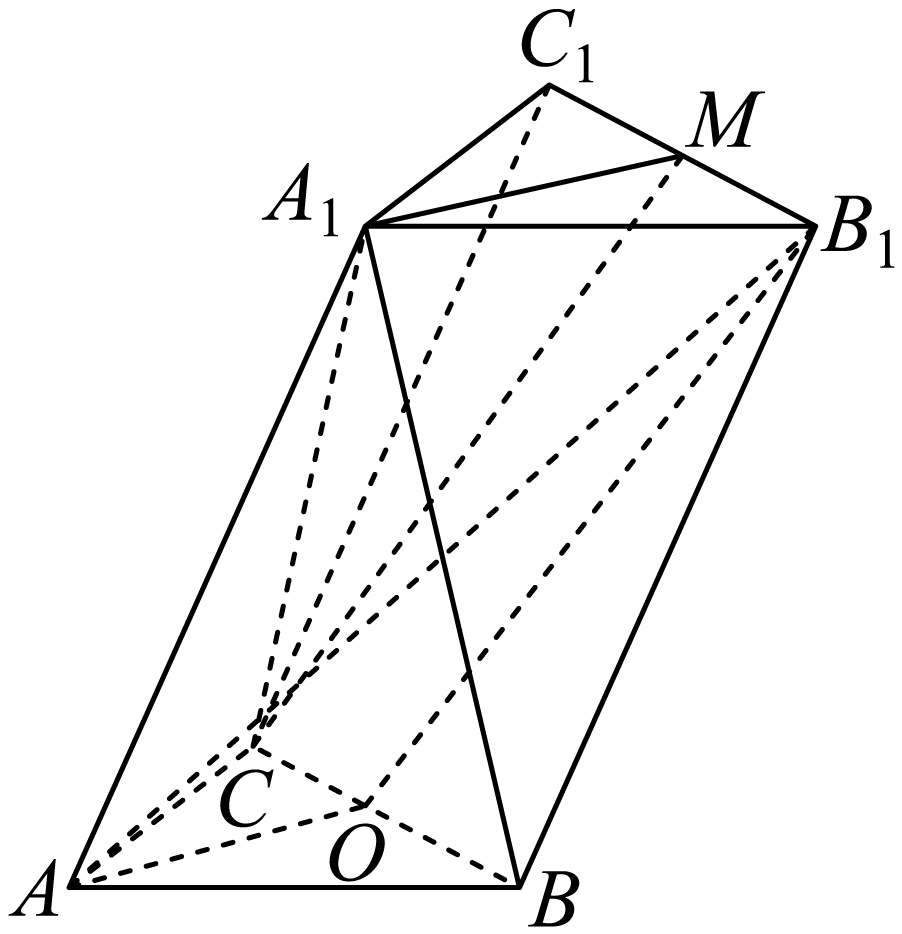
由$(1)$可知：${{A}_{1}}M//AO$，且${{A}_{1}}M\subset $平面${{A}_{1}}MC$，$AO\not\subset $平面${{A}_{1}}MC$，则$AO//$平面${{A}_{1}}MC$，

在平行四边形$BC{{C}_{1}}{{B}_{1}}$中，$O,M$分别为$BC,{{B}_{1}}{{C}_{1}}$的中点，则$OC//M{{B}_{1}}$，$OC=M{{B}_{1}}$，

四边形$CO{{B}_{1}}M$为平行四边形，$CM//O{{B}_{1}}$，且$CM\subset $平面${{A}_{1}}MC$，$O{{B}_{1}}\not\subset $平面${{A}_{1}}MC$，

于是$O{{B}_{1}}//$平面${{A}_{1}}MC$，且$AO\cap O{{B}_{1}}=O$，$AO,O{{B}_{1}}\subset $平面$AB_{1}O$，

$\therefore $ 平面${{A}_{1}}MC//$平面$AB_{1}O$，

且平面$A{{B}_{1}}O\cap $平面$ABC=AO$，则点$P$的轨迹为线段$AO$，即$AO=\sqrt{2}$，

由$AB\perp AC$，$AB=AC$，$O$为$BC$的中点，得$AB=AC=2,BC=2\sqrt{2}$，

$A{{A}_{1}}=2AB=4$，且$BC{{C}_{1}}{{B}_{1}}$为矩形，则${{S}_{BC{{C_1}}{{B}_{1}}}}=4\times 2\sqrt{2}=8\sqrt{2}$，

在$\triangle A{{A}_{1}}B$中，${{A}_{1}}B={{A}_{1}}A=4$，则$AB$边上的高$h=\sqrt{{{4}^{2}}-{{1}^{2}}}=\sqrt{15}$，

可得${{S}_{AB{{B_1}}{{A}_{1}}}}={{S}_{AC{{C_1}}{{A}_{1}}}}=2\times \sqrt{15}=2\sqrt{15}$，

$\therefore $ 三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$的侧面积$8\sqrt{2}+2\times 2\sqrt{15}=8\sqrt{2}+4\sqrt{15}$$.$