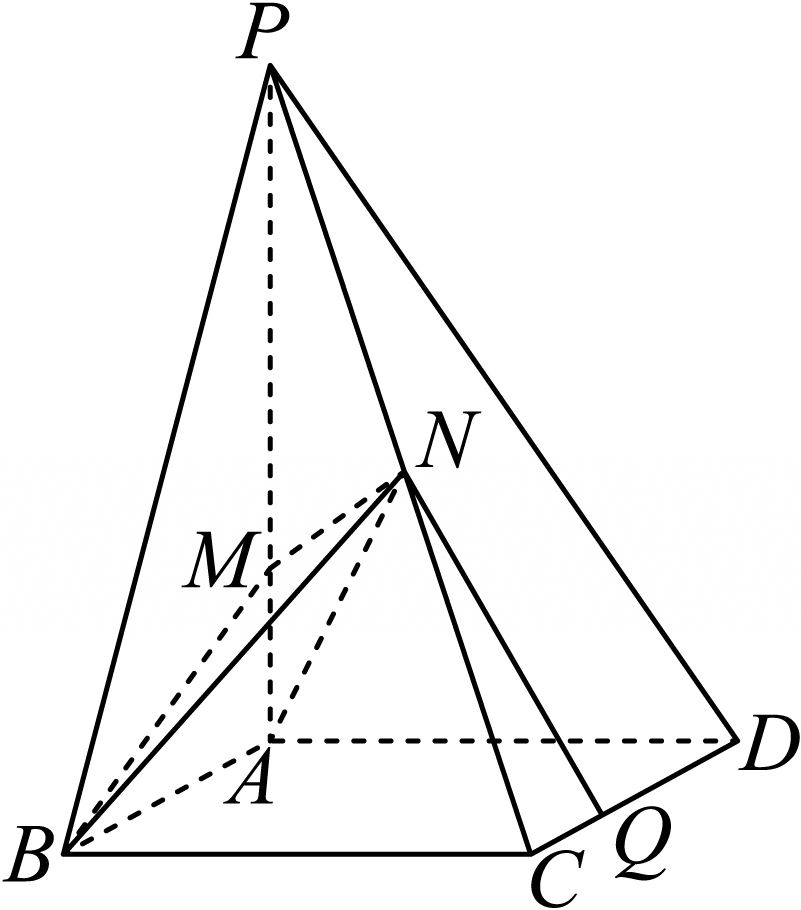
如图，在四棱锥$P-ABCD$中，底面$ABCD$是平行四边形，$PA\perp$底面$ABCD$，$\angle ABC=\dfrac{\pi }{3}$，$AB=1$，$BC=2$，$PA=3$，$M$，$N$分别是棱$PA$，$PC$上的点（含端点）．

$(1)$证明：$MN\perp CD$；

$(2)$若$N$为棱$PC$的中点，且二面角$A-MN-B$的正切值为$\dfrac{2\sqrt{3}}{3}$，求$AM$；

$(3)$设点$Q$是边$CD$上的点（含端点），求$2MN+NQ$的最小值．

$(1)$证明见解析；

$(2)1$；

$(3)$$2\\sqrt{3}$．

$(1)$证明：连接$AC$，

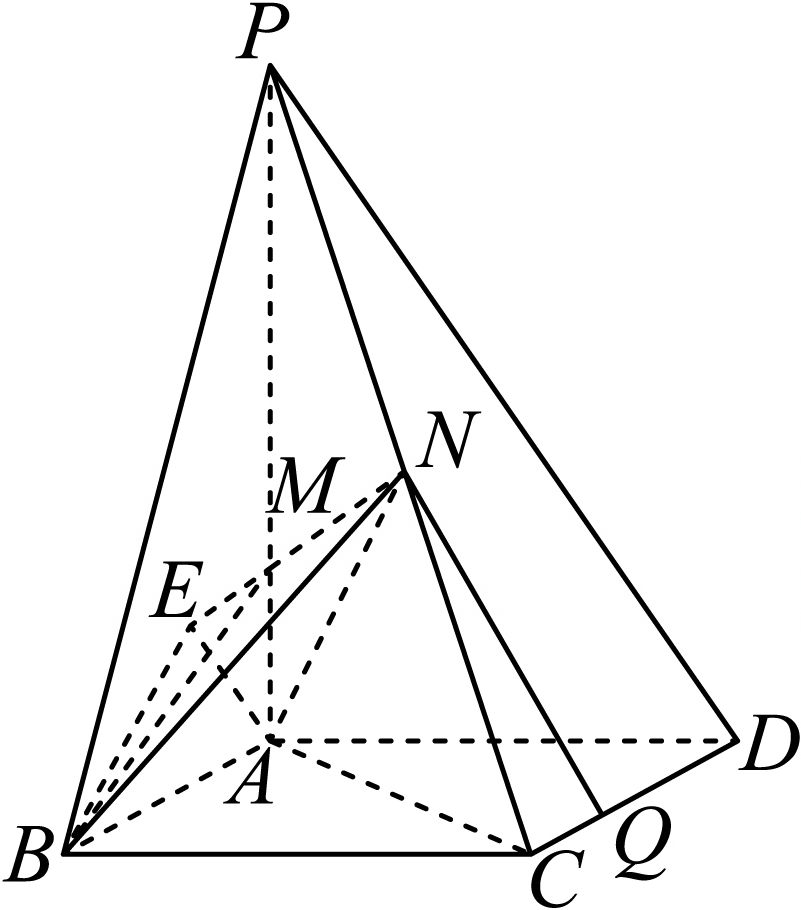
在$\triangle ABC$中，由余弦定理得，$\cos \angle ABC=\dfrac{{1}^{2}+{2}^{2}-A{C}^{2}}{4}=\dfrac{1}{2}\Rightarrow AC=\sqrt{3}$，

$\therefore AB^{2}+AC^{2}=1+3=BC^{2}$，

$\therefore \angle BAC=\dfrac{\pi }{2}$，

又$\because $ 四边形$ABCD$为平行四边形，

$\therefore \angle ACD=\dfrac{\pi }{2}$，即$AC\perp CD$，

$\because PA\perp$平面$ABCD$，$CD\subset$平面$ABCD$，

$\therefore PA\perp CD$，

又$PA\cap AC=A$，$PA$，$AC\subset$平面$PAC$，

$\therefore CD\perp$平面$PAC$，

又$MN\subset$平面$PAC$，

$\therefore MN\perp CD$；

$(2)$在平面$BMN$中，过点$B$作$BE\perp MN$，垂足为$E$，连接$AE$，

由$(1)$知，$AB\perp$平面$AMN$，$MN\subset$平面$AMN$，

$\therefore AB\perp MN$，

又$BE\cap BA=B$，$BE$，$BA\subset$平面$ABE$，

$\therefore MN\perp AE$，

又$BE\subset$平面$BMN$，$AE\subset$平面$AMN$，平面$BMN\cap$平面$AMN=MN$，

$\therefore \angle BEA$为二面角$A-MN-B$的平面角，

$\because AB\perp$平面$AMN$，$AE\subset$平面$AMN$，

$\therefore AB\perp AE$，

则在${\rm Rt}\triangle ABE$中，$\tan \angle AEB=\dfrac{AB}{AE}=\dfrac{1}{AE}=\dfrac{2\sqrt{3}}{3}\Rightarrow AE=\dfrac{\sqrt{3}}{2}$，

$\because PA\perp$底面$ABCD$，$AC\subset$平面$ABCD$，

$\therefore PA\perp AC$，

在$Rt$$\triangle $$PAC$中，$PC=\sqrt{P{A}^{2}+A{C}^{2}}=\sqrt{{3}^{2}+({\sqrt{3})}^{2}}=2\sqrt{3}$，

又$N$为棱$PC$的中点，

$\therefore AN=CN=\sqrt{3}$，

$\therefore AN=AC=CN$，则$\angle NAC=\dfrac{\pi }{3}$，

$\therefore \angle NAM=\dfrac{\pi }{2}-\dfrac{\pi }{3}=\dfrac{\pi }{6}$，

在${\rm Rt}\triangle AEN$中，$\sin \angle ANE=\dfrac{AE}{AN}=\dfrac{1}{2}\Rightarrow \angle ANE=\dfrac{\pi }{6}$，

$\therefore AM=MN$，设$AM=MN=x$，

在$\triangle AMN$中，由余弦定理得，$\cos \angle AMN=\dfrac{{x}^{2}+{x}^{2}-3}{2{x}^{2}}=-\dfrac{1}{2}\Rightarrow x=1$，

$\therefore AM=1$．

$(3)$将$\triangle PAC$，$\triangle PCD$在同一平面展开，将$\triangle PAC$沿$PA$对称得$\triangle PAC'$，点$N$沿$PA$对称得$N'$，

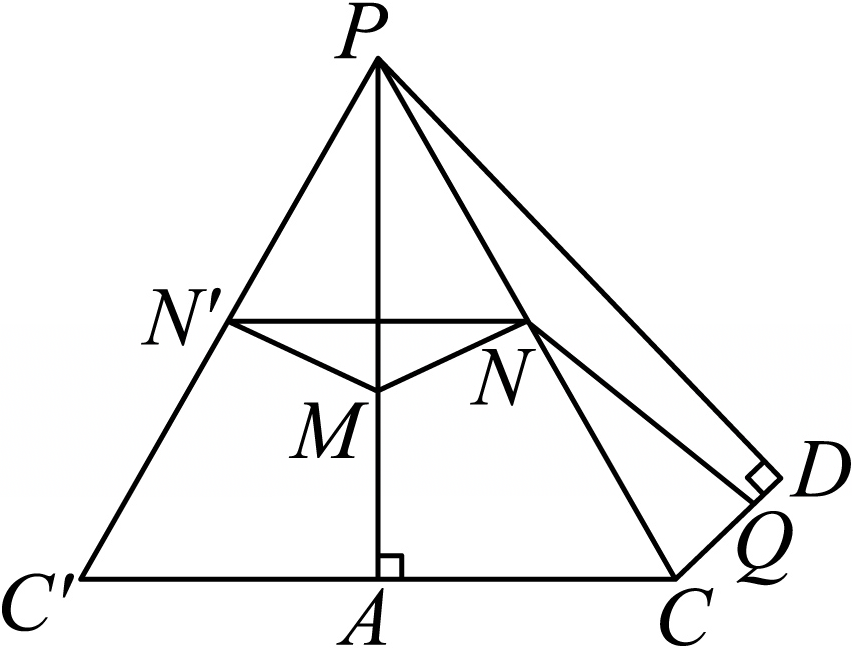
则$2MN=MN+MN' \geqslant NN'$，当且仅当$M$，$N$，$N'$在同一直线上时，取得最小值，

$\therefore 2MN+NQ\geqslant NN' +NQ$，

当$N$，$N'$，$Q$在同一直线上，且过点$C$时，取得最小值，如图所示，

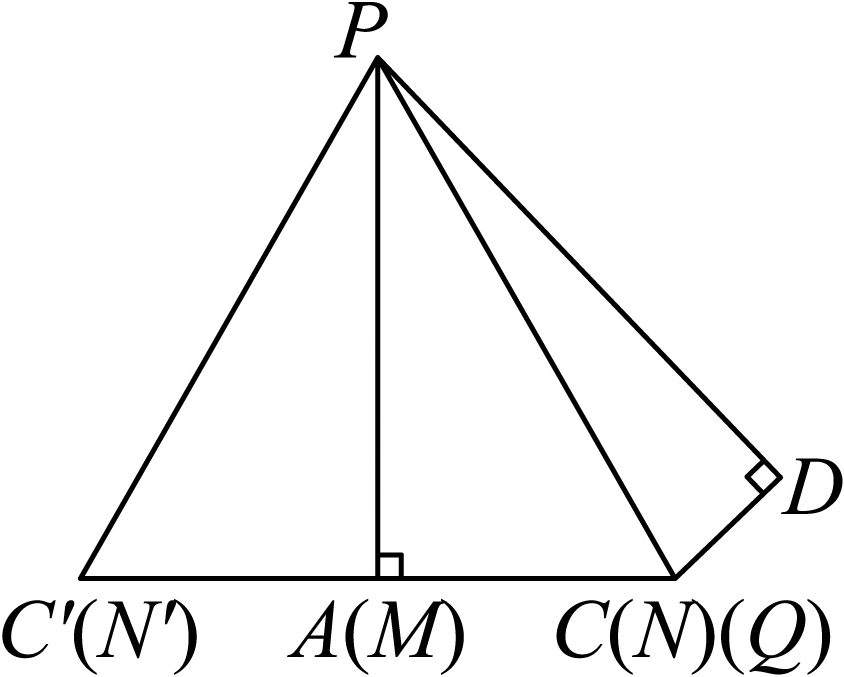
则$2MN+NQ\ge CC' =2AC=2\sqrt{3}$，

故$2MN+NQ$的最小值为$2\sqrt{3}$．