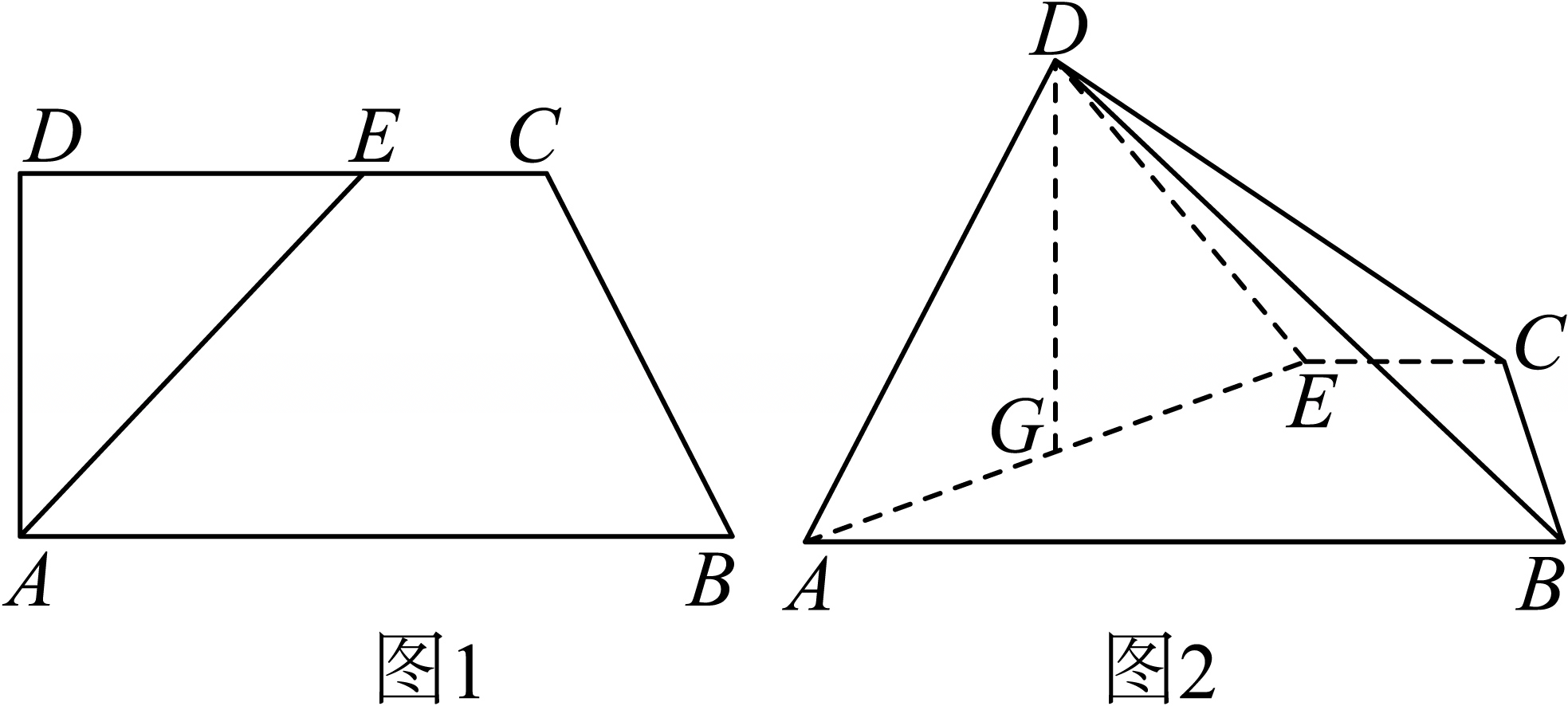
如图，在直角梯形$ABCD$中，$AB//DC$，$\angle BAD=90^\circ$，$AB=4$，$AD=2$，$DC=3$，点$E$在$CD$上，且$DE=2$，将$\triangle $$ADE$沿$AE$折起，使得$DB=2\sqrt{3}$（如图），$G$为$AE$中点．

$(1)$求证：$DG\perp$平面$ABCE$；

$(2)$求$BD$与平面$ABCE$的所成角；

$(3)$在线段$BD$上是否存在点$P$，使得$CP//$平面$ADE$？若存在，求$\dfrac{BP}{BD}$的值；若不存在，请说明理由．

$(1)$证明见解析；

$(2)$$\\arcsin \\dfrac{\\sqrt{6}}{6}$；

$(3)$$\\dfrac{3}{4}$

$(1)$连接$BG$，

$\because AD=DE=2$，$G$为$AE$中点，

$\therefore DG\perp AE$，

又$AD\perp DE$，

$\therefore AE=2\sqrt{2}$，

$\therefore DG=AG=\sqrt{2}$，

在$\triangle $$ABG$中，$AB=4$，$\angle BAD=90^\circ$，则$\angle BAG=\dfrac{\pi }{4}$，

$\therefore GB^{2}=2+16-2\times \sqrt{2}\times 4\times \cos \dfrac{\pi }{4}=18-8=10$，

又$\because BD=2\sqrt{3}$，$DG=\sqrt{2}$，

$\therefore BD^{2}=DG^{2}+GB^{2}$，则$DG\perp GB$，

又$AE\cap GB=G$，$AE$，$GB\subset$面$ABCE$，

$\therefore DG\perp$平面$ABCE$；

$(2)$由$(1)$知$\angle DBG$为$BD$与平面$ABCE$所成的角，

在${\rm Rt}$$\triangle $$DGB$中，$BD=2\sqrt{3}$，$DG=\sqrt{2}$，

$\therefore \sin \angle DBG=\dfrac{DG}{BD}=\dfrac{\sqrt{2}}{2\sqrt{3}}=\dfrac{\sqrt{6}}{6}$，

又$\angle DBG\in \left[0,\dfrac{\pi }{2}\right]$，

$\therefore \angle DBG=\arcsin \dfrac{\sqrt{6}}{6}$，

即$BD$与平面$ABCE$所成的角为$\arcsin \dfrac{\sqrt{6}}{6}$；

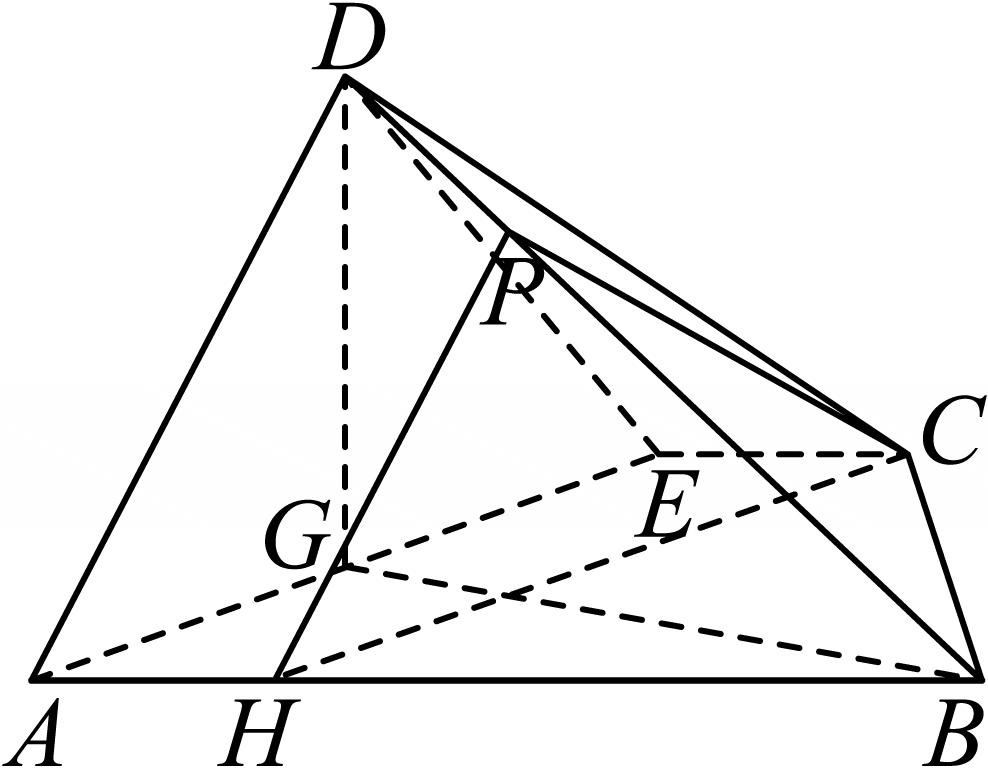
$(3)$存在，且$\dfrac{BP}{BD}=\dfrac{3}{4}$，理由如下，

如图在$AB$上取点$H$，使$AH=\dfrac{1}{4}AB=1$，连接$CH$，过$H$作$HP//AD$交$BD$于$P$，连接$CP$，

$\because CE//AH$，且$AH=CE=1$，

$\therefore $ 四边形$AHCE$为平行四边形，则$AE//HC$，

又$AE\subset$平面$ADE$，$HC\not\subset$平面$ADE$，

$\therefore HC//$平面$ADE$，

又$AD\subset$平面$ADE$，$HP\not\subset$平面$ADE$，

$\therefore HP//$平面$ADE$，

又$HP\cap HC=H$，$HP$，$HC\subset$平面$HPC$，

$\therefore $ 平面$ADE//$平面$HPC$，

又$PC\subset$平面$HPC$，

$\therefore PC//$平面$ADE$，

此时$\dfrac{BP}{BD}=\dfrac{BH}{AB}=\dfrac{3}{4}$，

$\therefore $ 在线段$BD$上是否存在点$P$，使得$CP//$平面$ADE$，且$\dfrac{BP}{BD}=\dfrac{3}{4}$．