如图，正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$棱长为$1$，$P$是$A_{1}D$上的一个动点，下列结论中正确的是$(\qquad)$．

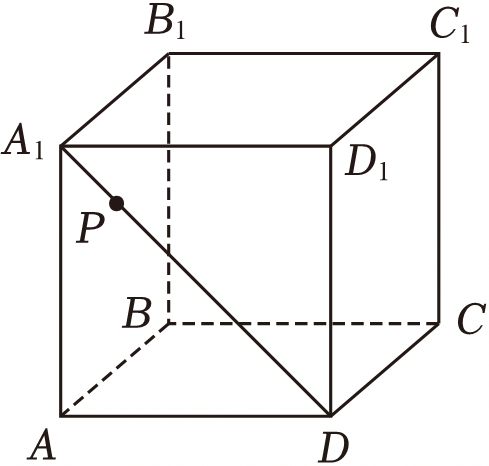
$BP$的最小值为$\\dfrac{\\sqrt{6}}{2}$

当$P$在$A_{1}D$上运动时，都有$C_{1}P\\perp BD_{1}$

当$P$在直线$A_{1}D$上运动时，三棱锥$A-B_{1}PC$的体积不变

$PA+PC$的最小值为$\\sqrt{2-\\sqrt{2}}$

对于$\rm A$，连接$A_{1}B$，$BD$，在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，${A}_{1}B=BD={A}_{1}D=\sqrt{2}$，

故$BP$的最小值为正三角形$A_{1}BD$的边$A_{1}D$上的高，即$\sqrt{2}\times \dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{6}}{2}$，$\rm A$正确；

对于$\rm B$，连接$A_{1}C_{1}$，$B_{1}D_{1}$，$DC_{1}$，

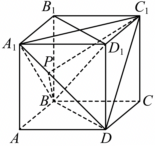
由于$BB_{1}\perp$平面$A_{1}B_{1}C_{1}D_{1}$，$A_{1}C_{1}\subset$平面$A_{1}B_{1}C_{1}D_{1}$，故$BB_{1}\perp A_{1}C_{1}$，

而$B_{1}D_{1}\perp A_{1}C_{1}$，$BB_{1}\cap B_{1}D_{1}=B_{1}$，$BB_{1}$，$B_{1}D_{1}\subset$平面$BB_{1}D_{1}$，

故$A_{1}C_{1}\perp$平面$BB_{1}D_{1}$，$BD_{1}\subset$平面$BB_{1}D_{1}$，故$A_{1}C_{1}\perp BD_{1}$；

同理可证$A_{1}D\perp BD_{1}$，$A_{1}D\cap A_{1}C_{1}=A_{1}$，$A_{1}D$，$A_{1}C_{1}\subset$平面$A_{1}DC_{1}$，

故$BD_{1}\perp$平面$A_{1}DC_{1}$，$C_{1}P\subset$平面$A_{1}DC_{1}$，故$BD_{1}\perp C_{1}P$，即$C_{1}P\perp BD_{1}$，$\rm B$正确；

对于$\rm C$，连接$AB_{1}$，$B_{1}C$，$AC$，

$\because A_{1}B_{1}//DC$，$A_{1}B_{1}=DC$，

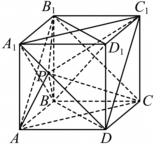
故四边形$A_{1}B_{1}CD$为平行四边形，则$A_{1}D//B_{1}C$，$B_{1}C\subset$平面$AB_{1}C$，$A_{1}D\not\subset$平面$AB_{1}C$，

故$A_{1}D//$平面$AB_{1}C$，$P$点在直线$A_{1}D$上运动，即$P$到平面$AB_{1}C$的距离为定值，

而$\triangle $$AB_{1}C$为边长为$\sqrt{2}$的正三角形，其面积为定值，

故三棱锥$P-AB_{1}C$的体积为定值，由于${V}_{A-{B_1}PC}={V}_{P-A{B_1}C}$，

故三棱锥$A-PB_{1}C$的体积为定值，$\rm C$正确；

对于$\rm D$，将平面$DCB_{1}A_{1}$沿着$A_{1}D$翻折到平面$AA_{1}D$上，连接$AC$，

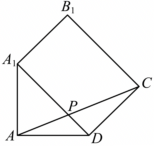
与$A_{1}D$交于点$P$，则$AC$即为$PA+PC$的最小值；

在$\triangle ADC$中，$\angle ADC=135^\circ$，$AC=\sqrt{AD^{2}+CD^{2}-2AD\cdot CD\cos 135^\circ }=\sqrt{2+\sqrt{2}}$，

即$PA+PC$的最小值为$\sqrt{2+\sqrt{2}}$，$\rm D$错误．

故选：$\rm ABC$