如图，在直三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，$A{{A}_{1}}=AB=AC=2,A{{A}_{1}}\perp AB$，$AC\perp AB,D$为${{A}_{1}}{{B}_{1}}$中点，$E$为$A{{A}_{1}}$中点，$F$为$CD$中点$.$

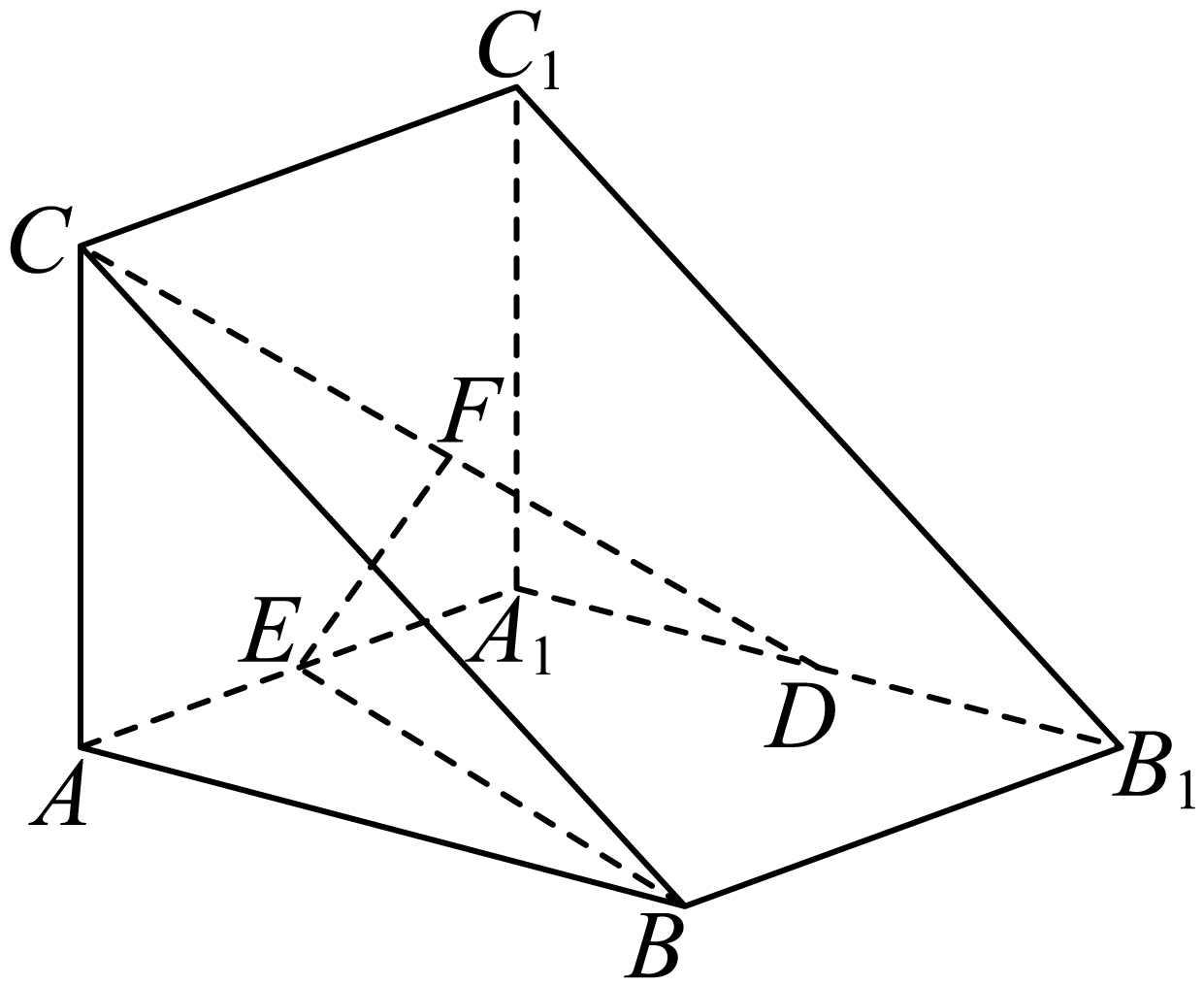
$(1)$求证$:$$EF//$平面$ABC$$;$

$(2)$求直线$BE$与平面$C{{C}_{1}}D$所成角的大小$.$

$(1)$证明见解析；

$(2)$$\\arcsin\\dfrac{4}{5}$

$(1)$

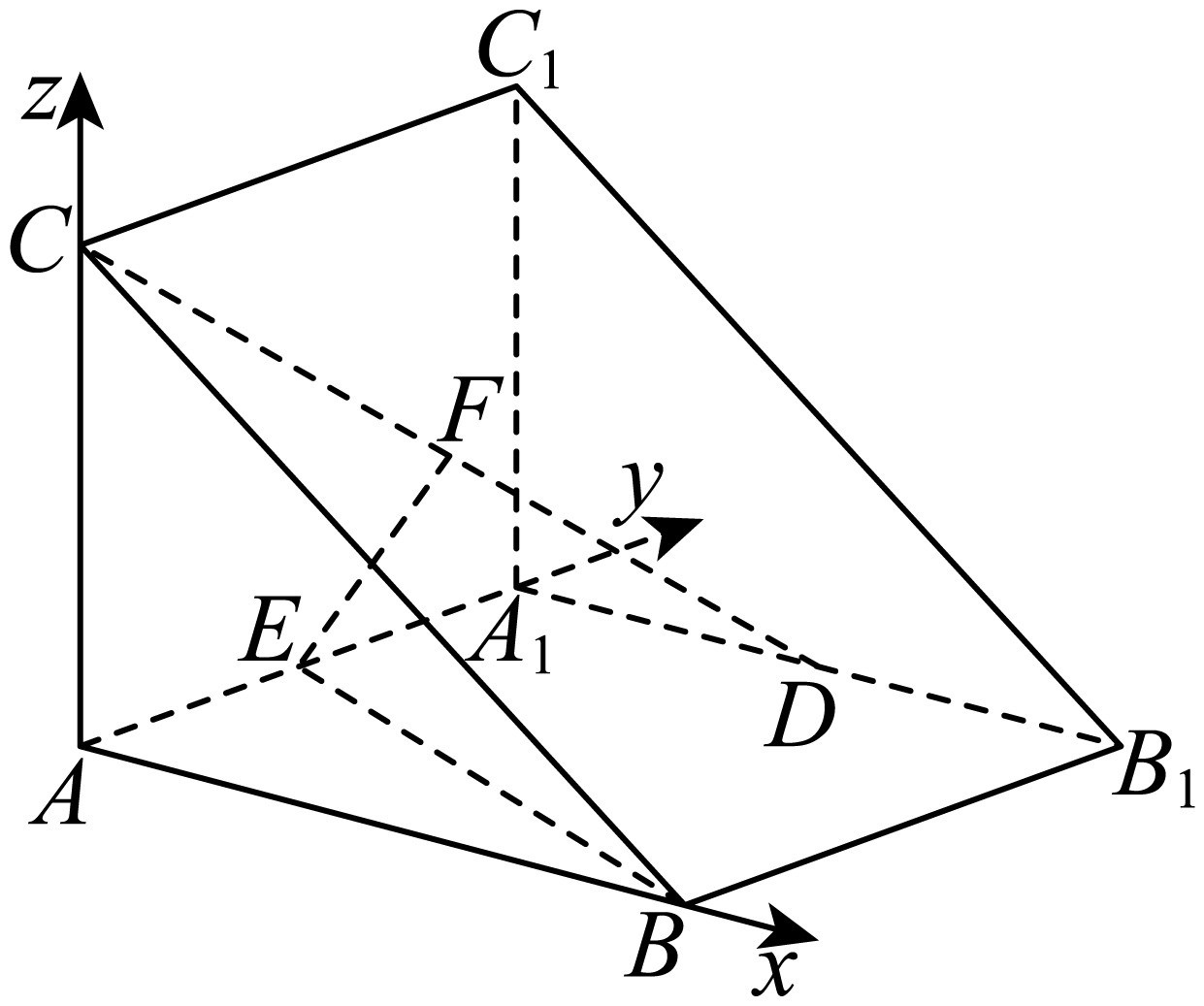
以$A$为原点，$\overrightarrow{AB},\overrightarrow{A{{A}_{1}}},\overrightarrow{AC}$为$x,y,z$正半轴方向建立空间直角坐标系，

则$B\left( 2\text{,}0\text{,}0 \right),C\left( 0\text{,}0\text{,}2 \right),{{A}_{1}}\left( 0\text{,}2\text{,}0 \right),{{B}_{1}}\left( 2\text{,}2\text{,}0 \right),{{C}_{1}}\left( 0\text{,}2\text{,}2 \right)$，

进而得$D\left( 1\text{,}2\text{,}0 \right),E\left( 0\text{,}1\text{,}0 \right),F\left( \dfrac{1}{2}\text{,}1\text{,}1 \right)$$.$

于是$\overrightarrow{EF}=\left( \dfrac{1}{2}\text{,}0\text{,}1 \right)$，而平面$ABC$的一个法向量$\boldsymbol{n}=\left( 0\text{,}1\text{,}0 \right)$$.$

由于$\overrightarrow{EF}\cdot \boldsymbol{n}=0$，且$EF\not\subset $平面$ABC$，因此$E F / /$平面$ABC$$.$

$(2)$由$(1)$知$\overrightarrow{BE}=\left( -2\text{,}1\text{,}0 \right)$，

设平面$C{{C}_{1}}D$的一个法向量$\boldsymbol{n}=\left( x,y,z \right)$$.$

由${{\overrightarrow{CC}}_{1}}=\left( 0\text{,}2\text{,}0 \right),\overrightarrow{{{C}_{1}}D}=\left( 1\text{,}0\text{,}-2 \right)$，

$\begin{cases} 2y=0 \\ x-2z=0 \\ \end{cases}$,

令$x=2$,则$y=0,z=1$，

$\therefore $ 平面$C{{C}_{1}}D$的一个法向量$\boldsymbol{n}=\left( 2\text{,}0\text{,}1 \right)$$.$

设直线$BE$与平面$C{{C}_{1}}D$所成角为$\theta $，则$\sin\theta =\dfrac{\left| \overrightarrow{BE}\cdot \boldsymbol{n} \right|}{\left| \overrightarrow{BE} \right|\left| {\boldsymbol{n}} \right|}=\dfrac{\left| -4+0+0 \right|}{\sqrt{5}\times \sqrt{5}}=\dfrac{4}{5}$，

因此直线$BE$与平面$C{{C}_{1}}D$所成角的大小为$\arcsin\dfrac{4}{5}$$.$