正四棱台的上下底面边长分别为$2$和$4$，侧棱长为$4$．

$(1)$求它的表面积；

$(2)$求它的体积．

$(1)$$20+12\\sqrt{15}$；$(2)$$\\dfrac{28}{3}\\sqrt{14}$．

如图：

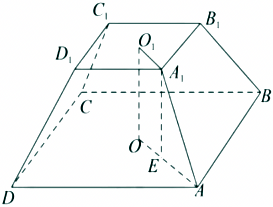
$(1)$正四棱台$ABCD-A_{1}B_{1}C_{1}D_{1}$，

等腰梯形$ABB_{1}A_{1}$的高为$\sqrt{{4}^{2}-{1}^{2}}=\sqrt{15}$，

则等腰梯形$ABB_{1}A_{1}$的面积为$\dfrac{(2+4)}{2}\times \sqrt{15}=3\sqrt{15}$，

$\therefore $ 正四棱台表面积为$S={2}^{2}+{4}^{2}+4\times 3\sqrt{15}=20+12\sqrt{15}$，

$(2)$在正四棱台$ABCD-A_{1}B_{1}C_{1}D_{1}$中，点$O_{1}$，$O$分别为上、下底面的中心，连接$OA$，$O_{1}A_{1}$，$OO_{1}$，

可得$OA=2\sqrt{2}$，${O}_{1}{A}_{1}=\sqrt{2}$，

过点$A_{1}$作$A_{1}E//OO_{1}$交$AO$于点$E$，则$A_{1}E\perp$底面$ABCD$，

进而得四边形$OEA_{1}O_{1}$为矩形，$OE={O}_{1}{A}_{1}=\sqrt{2}$，

$\therefore AE=2\sqrt{2}-\sqrt{2}=\sqrt{2}$，

$\therefore {A}_{1}E={O}_{1}O=\sqrt{A{ {A}}_{1}^{2}-A{E}^{2}}=\sqrt{14}$，即正四棱台的高为$\sqrt{14}$，

$\therefore $ 正四棱台的体积为$V=\dfrac{1}{3}\times \sqrt{14}\times (4+16+\sqrt{4\times 16})=\dfrac{1}{3}\sqrt{14}\times (20+8)=\dfrac{28\sqrt{14}}{3}$．