如图$1$，一个正四棱柱形的密闭容器水平放置，其底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有$a$升水时，水面恰好经过正四棱锥的顶点$P$．如果将容器倒置，水面也恰好过点$P$（图$2$），则$(\qquad)$．

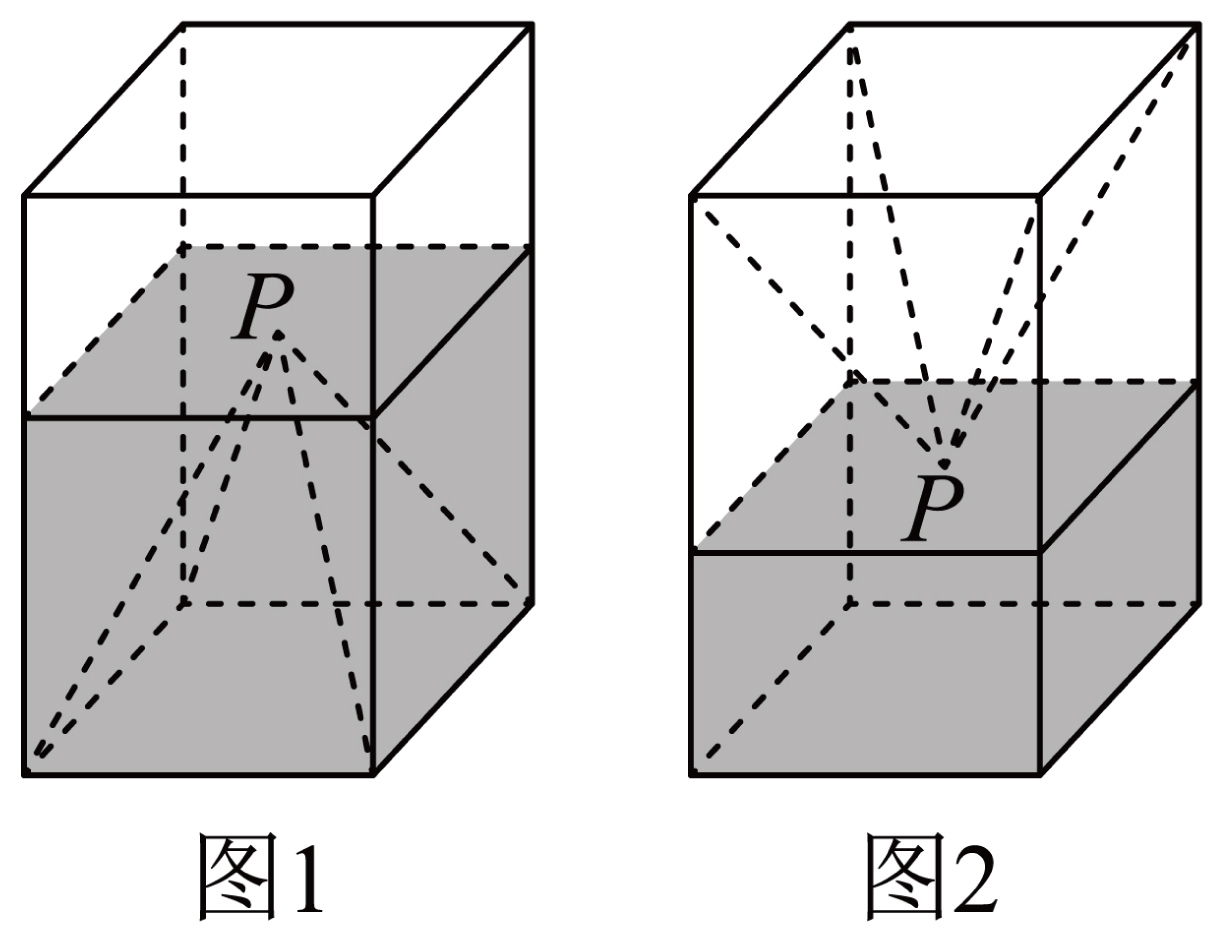
若往容器内再注入$a$升水，则容器恰好能装满

正四棱锥的高等于正四棱柱高的一半

将容器侧面水平放置时，水面也恰好过点$P$

任意摆放该容器，当水面静止时，水面都恰好经过点$P$

设图$1$中水的高度${{h}_{2}}$，几何体的高为${{h}_{1}}$，底面正方形的边长为$b$；

则图$2$中水的体积为${{b}^{2}}{{h}_{1}}-{{b}^{2}}{{h}_{2}}={{b}^{2}}({{h}_{1}}-{{h}_{2}})$，即$\dfrac{2}{3}{{b}^{2}}{{h}_{2}}={{b}^{2}}({{h}_{1}}-{{h}_{2}})$，解得${{h}_{1}}=\dfrac{5}{3}{{h}_{2}}$，

$\therefore $ 正四棱锥的高等于正四棱柱高的一半是错误的，即$\rm B$错误．

对于$A$，往容器内再注入$a$升水，水面将升高$\dfrac{2}{3}h_{2}$，则$h_{2}+\dfrac{2}{3}h_{2}=\dfrac{5}{3}h_{2}=h_{1}$，容器恰好能装满，$\rm A$正确；

对于$C$，当容器侧面水平放置时，$P$点在长方体中截面上，占容器内空间的一半，

$\therefore $ 水面也恰好经过$P$点，$\rm C$正确；

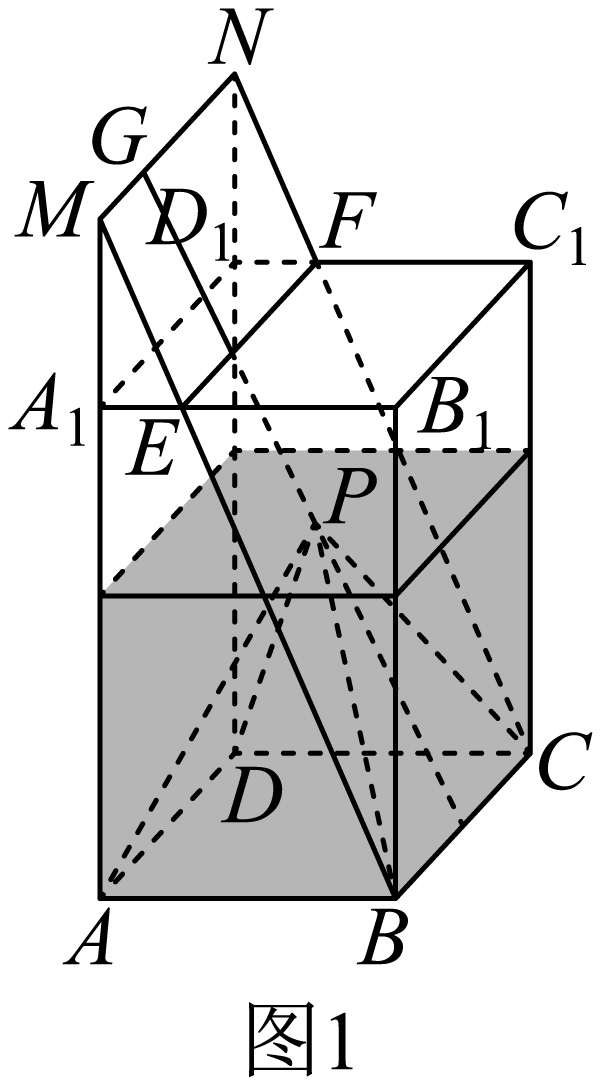
对于$D$中，如图所示，当水面与正四棱锥的一个侧面重合时，

$\because $ 四棱锥的高为${{h}_{2}}$，几何体的高度为${{h}_{1}}$，设正四棱柱的底面边长为$b$，

可得${{A}_{1}}M=\dfrac{1}{3}{{h}_{2}}$，由$\triangle {{A}_{1}}ME\backsim \triangle AMB$，可得$\dfrac{{{A}_{1}}M}{AM}=\dfrac{{{A}_{1}}E}{AB}$，可得${{A}_{1}}E=\dfrac{{{A}_{1}}M\cdot AB}{AM}=\dfrac{1}{6}b$，

$\therefore B{{B}_{1}}E-C{{C}_{1}}F$的体积为${{V}_{1}}=\dfrac{1}{2}\times \dfrac{5}{6}b\times {{h}_{1}}\times b=\dfrac{1}{2}\times \dfrac{5}{6}b\times \dfrac{5}{3}{{h}_{2}}\times b=\dfrac{25}{36}{{b}^{2}}{{h}_{2}}$，

可得水的体积为${{V}_{1}}=\dfrac{25}{36}{{b}^{2}}{{h}_{2}}$，此时$\dfrac{25}{36}{{b}^{2}}{{h}_{2}}\gt \dfrac{2}{3}{{b}^{2}}h_{2}^{{}}$，矛盾，

$\therefore \rm D$不正确$.$

故选：$\rm AC$．