（$24-25$高二上$·$上海宝山$·$期中）如图，在直三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，$AB=BC=\sqrt{2}$，$AC=AA_{1}=2$，且$D$、$E$分别是$AC$、${{A}_{1}}{{C}_{1}}$的中点$.$

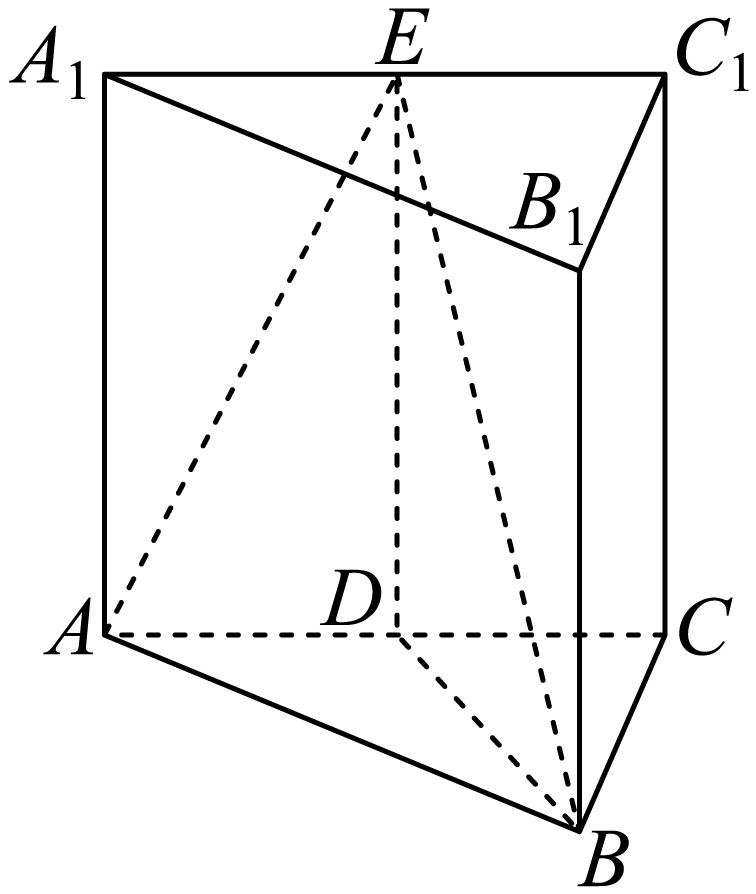
$(1)$求直三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$的全面积；

$(2)$求三棱锥$D-ABE$的体积：

$(3)$求直线$BD$与平面$ABE$所成角的大小$.$（结果用反三角函数值表示）

$(1)$$4\\sqrt{2}+6$；

$(2)$$\\dfrac{1}{3}$；

$(3)$$\\arcsin \\dfrac{2}{3}$$.$

$(1)$在直三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，$AB=BC=\sqrt{2}$，$AC=AA_{1}=2$，

由$A{{B}^{2}}+B{{C}^{2}}=4=A{{C}^{2}}$，得$\angle ABC={{90}^{^\circ }}$，

该棱柱的两底面积为$2{{S}_{\triangle ABC}}=2\times \dfrac{1}{2}A{{B}^{2}}=2$，侧面积为$(AB+BC+AC)A{{A}_{1}}=4\sqrt{2}+4$，

$\therefore $ 直三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$的全面积为$4\sqrt{2}+6$$.$

$(2)$在直三棱柱$ABC-{{A}_{1}}{{B}_{1}}{{C}_{1}}$中，由$D,E$分别是$AC,{{A}_{1}}{{C}_{1}}$的中点，得$ED//{{A}_{1}}A$，

而${{A}_{1}}A\perp $平面$ABC$，则$ED\perp $平面$ABC$，由$(1)$知，${{S}_{\triangle ABD}}=\dfrac{1}{2}{{S}_{\triangle ABC}}=\dfrac{1}{2}$，

又$DE=A{{A}_{1}}=2$，则${{V}_{E-ABD}}=\dfrac{1}{3}{{S}_{\triangle ABD}}\cdot DE=\dfrac{1}{3}\times \dfrac{1}{2}\times 2=\dfrac{1}{3}$，而${{V}_{D-ABE}}={{V}_{E-ABD}}$，

$\therefore $ 三棱锥$D-ABE$的体积为$\dfrac{1}{3}$$.$

$(3)$由$(2)$知${{V}_{D-ABE}}=\dfrac{1}{3}$，设点$D$到面$ABE$的距离为$d$，

$\triangle ABE$中，$AB=\sqrt{2}$，$AE=BE=\sqrt{{{2}^{2}}+{{1}^{2}}}=\sqrt{5}$，${{S}_{\triangle ABE}}=\dfrac{1}{2}\times \sqrt{2}\times \sqrt{5-{{\left(\dfrac{\sqrt{2}}{2}\right)}^{2}}}=\dfrac{3}{2}$，

由${{V}_{D-ABE}}=\dfrac{1}{3}{{S}_{\triangle ABE}}\cdot d=\dfrac{1}{3}$，得$d=\dfrac{2}{3}$，设直线$BD$与平面$ABE$所成角为$\alpha $，则$\sin\alpha =\dfrac{d}{BD}=\dfrac{2}{3}$，

$\therefore $ 直线$BD$与平面$ABE$所成角的大小为$\arcsin \dfrac{2}{3}$$.$