已知函数$f(x)=\dfrac{a{{x}^{2}}-1}{{{\text{e}}^{x}}}$．

$(1)$若函数${{f}({x})}$单调递增，求实数$a$的取值范围；

$(2)$若函数$g(x)=(f(x)+1){{\text{e}}^{x}}$只有一个极值点，求实数$a$的取值范围．

$(1)$$\\left\\{ a\\left| -1\\le a\\le 0 \\right. \\right\\}$

$(2)$$\\left\\{ a\\left| a\\gt 0 \\right. \\right\\}$

$(1)$根据题意，$f(x)=\dfrac{a{{x}^{2}}-1}{{{\text{e}}^{x}}}$，$x\in \mathbf{R}$，则${f}'(x)=\dfrac{-a{{x}^{2}}+2ax+1}{{{\text{e}}^{x}}}$，

若函数${{f}({x})}$单调递增，等价于${f}'(x)\ge 0$对任意$x\in \mathbf{R}$恒成立，

则$-a{{x}^{2}}+2ax+1\ge 0$，即$a{{x}^{2}}-2ax-1\le 0$，

当$a=0$时，$-1\lt 0$，符合题意；

当$a\ne 0$时，可得$\begin{cases} a\lt 0 \\ \varDelta=4{{a}^{2}}+4a\le 0 \\ \end{cases}$，解得$-1\le a\lt 0$；

综上所述：$a$的取值范围为$\left\{ a\left| -1\le a\le 0 \right. \right\}$$.$

$(2)$依题意，$g(x)=(f(x)+1){{\text{e}}^{x}}=a{{x}^{2}}-1+{{\text{e}}^{x}}$，则${g}'\left( x \right)=2ax+{{\text{e}}^{x}}$只有一个变号零点，

显然$x=0$不是${g}'\left( x \right)$的零点，

$\therefore 2ax+{{\text{e}}^{x}}=0\Leftrightarrow -2a=\dfrac{{{\text{e}}^{x}}}{x}$有一个变号交点，

令$h\left( x \right)=\dfrac{{{\text{e}}^{x}}}{x}\Leftrightarrow {h}'\left( x \right)=\dfrac{{{\text{e}}^{x}}x-{{\text{e}}^{x}}}{{{x}^{2}}}=\dfrac{{{\text{e}}^{x}}}{{{x}^{2}}}\left( x-1 \right)$，

可知函数$h(x)$在$(-\infty,0)$和$(0,1)$分别单调递减，在$(1,+\infty )$上单调递增，

$h(1)=\text{e}$，且当$x\to {{0}^{+}}$或$+\infty $时，$h(x)\to +\infty $，当$x\to {{0}^{-}}$时，$h(x)\rightarrow -\infty$，当$x\to -\infty $时，$h(x) \rightarrow 0$，

如图象所示，

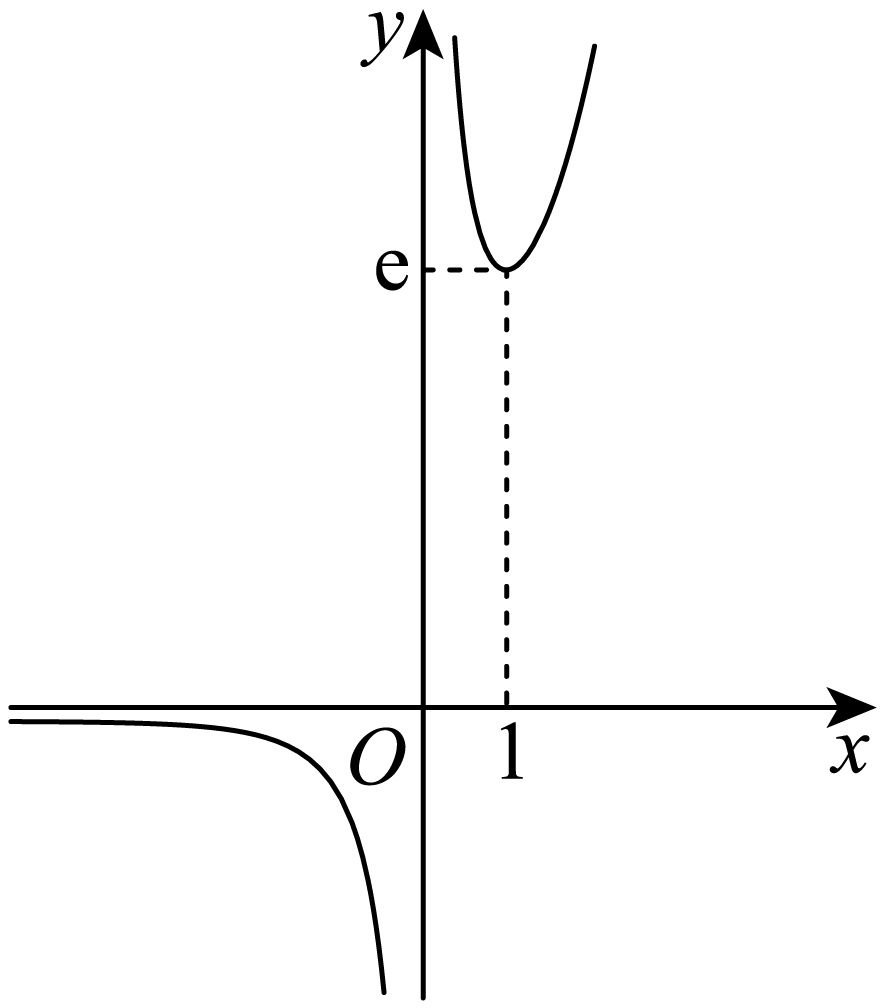
可得：$-2a\lt 0\Leftrightarrow a\gt 0$，

$\therefore $ $a$的取值范围为$\left\{ a\left| a\gt 0 \right. \right\}$$.$