幂函数$y={{x}^{\alpha }}$，当$\alpha $取不同的正数时，在区间$\left\lbrack {0,1}\right\rbrack$上它们的图像是一族美丽的曲线（如图）．设点$A\left( 1,0 \right)$，$B\left( 0,1 \right)$，连接$AB$，线段$AB$恰好被其中的两个幂函数$f\left( x \right)={{x}^{a}}$，$g\left( x \right)={{x}^{b}}$的图像三等分，即有$AN=NM=MB$．

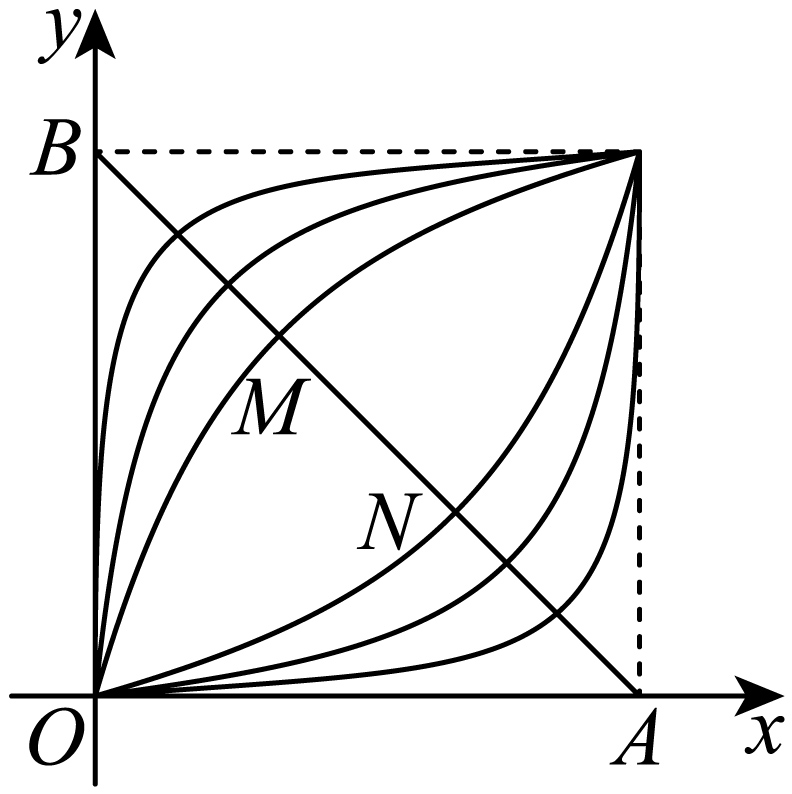
$(1)$写出点$M$、$N$的坐标并求$ab$的值；

$(2)$函数$h\left( x \right)={{\text{e}}^{abx}}-{{\text{e}}^{-abx}}$．

$($i$)$指明函数单调性和奇偶性（无需证明）；

$($ⅱ$)$若对任意$x\gt 0$，$\theta \in \left[ 0,\dfrac{\pi}{2} \right]$，不等式：$h\left( \left( {{t}^{2}}-1 \right)x \right)+h\left( t\left( {{x}^{2}}+2 \right)\sin \left( \theta +\dfrac{5\pi}{4} \right) \right)\leqslant 0$恒成立，求正数$t$的取值范围．

$(1)$$M\\left( \\dfrac{1}{3},\\dfrac{2}{3} \\right)$，$N\\left( \\dfrac{2}{3},\\dfrac{1}{3} \\right)$，$ab=1$；

$(2)$$($i$)$答案见解析；$($ⅱ$)$$0\\lt t\\leqslant 1+\\sqrt{2}$

$(1)$由图可得$M\left( \dfrac{1}{3},\dfrac{2}{3} \right)$，$N\left( \dfrac{2}{3},\dfrac{1}{3} \right)$，

$∴{{\left( \dfrac{1}{3} \right)}^{a}}=\dfrac{2}{3}$，${{\left( \dfrac{2}{3} \right)}^{b}}=\dfrac{1}{3}$，

$∴$$a={{\log }_{\tfrac{1}{3}}}\dfrac{2}{3}$，$b={{\log }_{\tfrac{2}{3}}}\dfrac{1}{3}$，

$∴$$ab={{\log }_{\tfrac{1}{3}}}\dfrac{2}{3}\times {{\log }_{\tfrac{2}{3}}}\dfrac{1}{3}=\dfrac{\lg \dfrac{2}{3}}{\lg \dfrac{1}{3}}\times \dfrac{\lg \dfrac{1}{3}}{\lg \dfrac{2}{3}}=1$；

$(2)$$($i$)$由$(1)$可知$h\left( x \right)={{\text{e}}^{x}}-{{\text{e}}^{-x}}$，$h\left( x \right)$定义域为$\mathbf{R}$，

$y={{\text{e}}^{x}}$和$y=-{{\text{e}}^{-x}}=-{{\left( \dfrac{1}{\text{e}} \right)}^{x}}$都是$\mathbf{R}$上的单调递增函数，

可知$h\left( x \right)$是定义在$\mathbf{R}$上的单调递增函数，

又$h\left( -x \right)={{\text{e}}^{-x}}-{{\text{e}}^{x}}=-h\left( x \right)$，可知$h\left( x \right)$为奇函数；

$($ⅱ$)$$h\left( x \right)$是定义在$\mathbf{R}$上的单调递增的奇函数可知

$h\left[ \left( {{t}^{2}}-1 \right)x \right]+h\left[ t\left( {{x}^{2}}+2 \right)\sin \left( \theta +\dfrac{5\pi}{4} \right) \right]\leqslant 0$恒成；

即$h\left[ \left( {{t}^{2}}-1 \right)x \right]\leqslant -h\left[ t\left( {{x}^{2}}+2 \right)\sin \left( \theta +\dfrac{5\pi}{4} \right) \right]$恒成立；

即$h\left[ \left( {{t}^{2}}-1 \right)x \right]\leqslant h\left[ t\left( {{x}^{2}}+2 \right)\sin \left( \theta +\dfrac{\pi}{4} \right) \right]$恒成立；

即$\left( {{t}^{2}}-1 \right)x\leqslant t\left( {{x}^{2}}+2 \right)\sin \left( \theta +\dfrac{\pi}{4} \right)$恒成立；

即$\dfrac{{{t}^{2}}-1}{t}\leqslant \left( x+\dfrac{2}{x} \right)\sin \left( \theta +\dfrac{\pi}{4} \right)$恒成立．

又$x+\dfrac{2}{x}\geqslant 2\sqrt{2}$，当且仅当$x=\sqrt{2}$时等号成立．

由$\theta \in \left[ 0,\dfrac{\pi}{2} \right]$可得：$\theta +\dfrac{\pi}{4}\in \left[ \dfrac{\pi}{4},\dfrac{3\pi}{4} \right]$，

$∴$$\sin \left( \theta +\dfrac{\pi}{4} \right)\in \left[ \dfrac{\sqrt{2}}{2},1 \right]$，

$∴\left( x+\dfrac{2}{x} \right)\sin \left( \theta +\dfrac{\pi}{4} \right)\geqslant 2\sqrt{2}\times \dfrac{\sqrt{2}}{2}=2$当且仅当$x=\sqrt{2}$，$\theta =0$或$\dfrac{\pi}{2}$时等号成立，

$∴$$\dfrac{{{t}^{2}}-1}{t}\leqslant \left( x+\dfrac{2}{x} \right)\sin \left( \theta +\dfrac{\pi}{4} \right)$恒成立等价于$\dfrac{{{t}^{2}}-1}{t}\leqslant 2$．

$∴$$\dfrac{{{t}^{2}}-1}{t}\leqslant 2$且$t\gt 0$，

$∴$$\begin{cases} {{t}^{2}}-2t-1\leqslant 0 \\ t\gt 0 \\ \end{cases}$，解得$0\lt t\leqslant 1+\sqrt{2}$．