高中 | 描述圆周运动的物理量 题目答案及解析
稿件来源:高途
高中 | 描述圆周运动的物理量题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.4 圆周运动
描述圆周运动的物理量
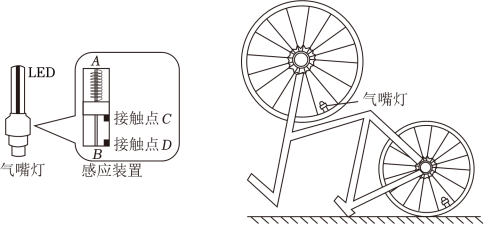
气嘴灯安装在自行车的气嘴上,骑行时会发光,一种气嘴灯的感应装置结构如图所示,感应装置内壁光滑,质量为$m$的重物套在光滑杆上,一端通过劲度系数为$k$的弹簧连在$A$点,重物上有触点$C$,在$B$端固定有触点$D$,如图重物静止时$C$、$D$间的距离$\Delta x=\dfrac{3mg}{k}$。当触点$C$、$D$接触后,$LED$灯就会发光,测得自行车车轮内径为$R$。让安装了气嘴灯的自行车倒放在地面上,旋转前车轮研究$LED$发光情况。重力加速度大小为$g$。气嘴灯大小相对车轮内径可忽略不计。
 $?$
$?$
若前轮匀速转动时,线速度大小${{v}_{0}}=\sqrt{5gR}$
①当气嘴灯运动到最低点时,求$B$端对重物的支持力;
②通过计算判断$LED$灯是否能一直发光;
若前轮匀速转动时,线速度大小${{v}_{0}}=\\sqrt{5gR}$当气嘴灯运动到最低点时,$B$端对重物的支持力为$2mg$;通过计算判断$LED$灯恰能一直发光;
"]]由离心运动的原理,可知$B$端应在车轮转轴外侧,更靠近气嘴,$A$端应在内侧,重物静止时,弹簧弹力${{F}_{1}}=mg=kx$
在最低点时,$B$端对重物的支持力为$F$,合力提供向心力,由牛顿第二定律得:$F+k(x+\Delta x)-mg=m\dfrac{v_{0}^{2}}{R}$
解得:$F=2mg$,方向竖直向上;
当气嘴灯运动到最高点时恰能发光,则此时的弹簧弹力为:
${{F}_{2}}=k(\Delta x+x)=4mg$
则此时的临界状态是弹簧弹力和其重力提供向心力,由牛顿第二定律得:${{F}_{2}}+mg=m\dfrac{{{v}^{2}}}{R}$
解得:$v=\sqrt{5gR}={{v}_{0}}$
则$LED$灯是恰能一直发光;
若使前轮匀速转动一周,线速度大小${{v}_{1}}=\dfrac{3\sqrt{2gR}}{2}$,求$LED$灯发光的时间。
若使前轮匀速转动一周,线速度大小${{v}_{1}}=\\dfrac{3\\sqrt{2gR}}{2}$,$LED$灯发光的时间为$\\dfrac{2\\pi \\sqrt{2}gR}{3g}$。
"]]由${{v}_{1}}=\dfrac{3\sqrt{2gR}}{2}\gt {{v}_{0}}$,当车速较大时,车轮转速较大,重物随这轮转动需要向心力较大,弹簧弹力变大,形变量变大,触电$C$与触点$D$接触,所以$LED$一直发光,前轮匀速转动一周,$LED$灯发光的时间为:$T=\dfrac{2\pi R}{{{v}_{1}}}$
解得:$T=\dfrac{2\pi \sqrt{2}gR}{3g}$。
高中 | 描述圆周运动的物理量题目答案及解析(完整版)
