用频闪照相记录平抛小球在不同时刻的位置，探究平抛运动的特点。

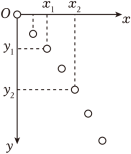
某同学实验时忘了标记重垂线方向，为解决此问题，他在频闪照片中，以某位置为坐标原点，沿任意两个相互垂直的方向作为$x$轴和$y$轴正方向，建立直角坐标系$xOy$，并测量出另外两个位置的坐标值$({{x}_{1}}$，${{y}_{1}})$、$({{x}_{2}}$，${{y}_{2}})$，如图所示。根据平抛运动规律，利用运动的合成与分解的方法，可得重垂线方向与$y$轴间夹角的正切值为                 。

如图${{x}_{0}}$、${{y}_{0}}$分别表示水平和竖直方向，设重垂线方向${{y}_{0}}$与$y$轴间的夹角为$\theta $，建立坐标系存在两种情况，如图所示：

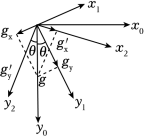
当建立的坐标系为${{x}_{1}}$、${{y}_{1}}$时，则$x$轴方向做匀减速运动；

根据逐差法计算加速度有${{x}_{2}}-2{{x}_{1}}=-g\sin \theta {{(2\;\rm T)}^{2}}$

$y$轴方向有${{y}_{2}}-2{{y}_{1}}=g\cos \theta {{(2\;\rm T)}^{2}}$

联立解得$\tan \theta =\dfrac{2{{x}_{1}}-{{x}_{2}}}{{{y}_{2}}-2{{y}_{1}}}$

当建立的坐标系为${{x}_{2}}$、${{y}_{2}}$时，则$x$轴方向做匀加速运动；

根据逐差法计算加速度有${{x}_{2}}-2{{x}_{1}}=g\sin \theta {{(2\;\rm T)}^{2}}$

$y$轴方向有${{y}_{2}}-2{{y}_{1}}=g\cos \theta {{(2\;\rm T)}^{2}}$

综上所述，重垂线方向与$y$轴间夹角的正切值为$\tan \theta =|\dfrac{2{{x}_{1}}-{{x}_{2}}}{{{y}_{2}}-2{{y}_{1}}}|$

故答案为：$|\dfrac{2{{x}_{1}}-{{x}_{2}}}{{{y}_{2}}-2{{y}_{1}}}|$