高中 | 探究平抛运动的特点 题目答案及解析
稿件来源:高途
高中 | 探究平抛运动的特点题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.3 实验:研究平抛运动
探究平抛运动的特点
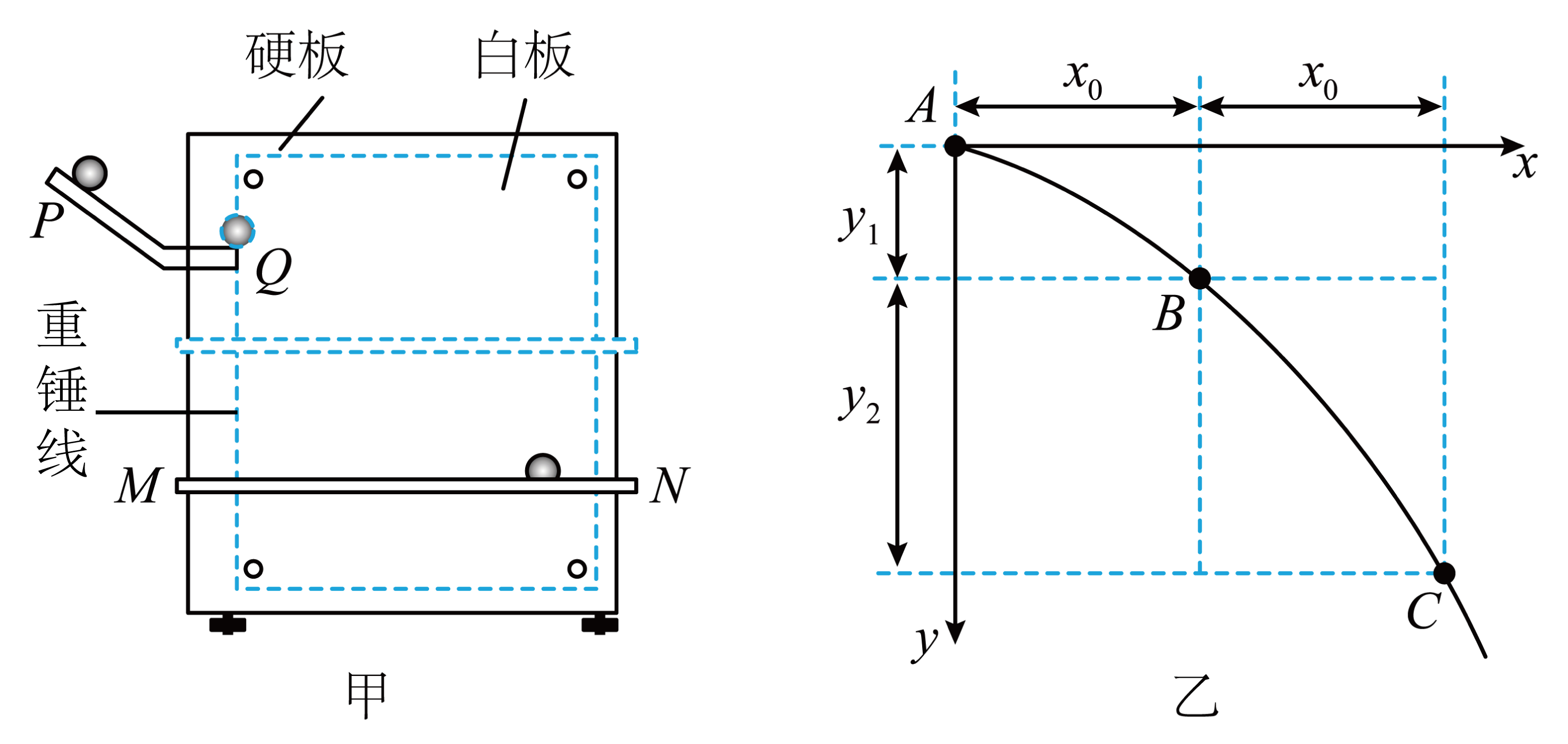
在“探究平抛运动的特点”实验中,某学习小组用如图甲所示装置研究平抛运动。将白纸和复写纸对齐重叠并固定在竖直的硬板上。钢球沿斜槽轨道$PQ$滑下后从$Q$点飞出,落在水平挡板$MN$上。由于挡板靠近硬板一侧较低,钢球落在挡板上时,钢球侧面会在白纸上挤压出一个痕迹点。移动挡板,重新释放钢球,如此重复,白纸上将留下一系列痕迹点。(已知当地重力加速度为$g$)
下列实验条件必须满足的有$(\quad\ \ \ \ )$(填标号);
斜槽轨道光滑
","斜槽轨道末段水平
","每次从斜槽上相同位置无初速度释放钢球
","图中挡条$MN$每次必须等间距下移
"]$\rm AC$.为了保证每次小球抛出的速度相同,每次从斜槽上相同位置无初速度释放钢球,但斜槽轨道不需要光滑,故$\rm A$错误,$\rm C$正确;
$\rm B$.为了保证小球抛出时的速度处于水平方向,斜槽轨道末段需要调节水平,故$\rm B$正确;
$\rm D$.图中挡条$MN$每次不需要等间距下移,故$\rm D$错误。
故选:$\rm BC$。
如图乙所示,在描出的轨迹上取$A$,$B$,$C$三点,$AB$和$BC$的水平间距相等且均为$x_{0}$,竖直间距分别是$y_{1}$和$y_{2}$,若$A$点是抛出点,则$\dfrac{y_{1}}{y_{2}} =$ ;钢球平抛的初速度大小为 (结果用上述字母表示):
$AB$和$BC$的水平间距相等且均为$x_{0}$,可知$AB$和$BC$所用时间相等,若$A$点是抛出点,则有$y_{1}=\dfrac{1}{2}gT^{2}$,$y_{1}+y_{2}=\dfrac{1}{2}g{(2T)}^{2}$
联立可得$\dfrac{y_{1}}{y_{2}}=\dfrac{1}{3}$
竖直方向有$\Delta y=y_{2} − y_{1}=gT^{2}$
解得$T=\sqrt{\dfrac{y_{2}-y_{1}}{g}}$
水平方向有$x_{0}=v_{0}T$
解得钢球平抛的初速度大小为$v_{0}=x_{0}\sqrt{\dfrac{g}{y_{2}-y_{1}}}$
如图乙所示,若$A$点不是抛出点,以$A$点为坐标原点,沿水平和竖直方向建立平面直角坐标系,在描出的轨迹上取$A$、$B$、$C$三点,$AB$和$BC$的水平间距相等且均为$x_{0}$,竖直间距分别是$y_{1}$和$y_{2}$,则$\dfrac{y_{1}}{y_{2}}$ $\dfrac{1}{3}$(填“大于”“等于”或“小于”);则小球抛出点的横坐标 (填“能”或“不能”)用$x_{0}$,$y_{1}$,$y_{2}$,$g$表示;纵坐标 (填“能”或“不能”)用$x_{0}$,$y_{1}$,$y_{2}$,$g$表示。
若$A$点不是抛出点,则有$y_{1}=v_{Ay}T+\dfrac{1}{2}gT^{2}$,$y_{1}+y_{2}=v_{Ay} \cdot 2T+ \dfrac{1}{2}g{(2T)}^{2}$
可得$y_{2}=v_{Ay}T+\dfrac{3}{2}gt^{2}$
则有$\dfrac{y_{1}}{y_{2}}=\dfrac{v_{Ay}T+\dfrac{1}{2}gT^{2}}{v_{Ay}T+\dfrac{3}{2}gT^{2}} \gt \dfrac{v_{Ay}T+\dfrac{1}{2}gT^{2}}{3v_{Ay}T+\dfrac{3}{2}gT^{2}}=\dfrac{1}{3}$
根据$\Delta y=y_{2} − y_{1}=gT^{2}$
解得$T=\sqrt{\dfrac{y_{2}-y_{1}}{g}}$
钢球平抛的初速度大小为$v_{0}=\dfrac{x_{0}}{T}=x_{0}\sqrt{\dfrac{g}{y_{2}-y_{1}}}$
小球经过$B$点的竖直分速度为$v_{By}=\dfrac{y_{AC}}{2T}=\dfrac{y_{1}+y_{2}}{2}\sqrt{\dfrac{g}{y_{2}-y_{1}}}$
根据$v_{By}=gt_{B}$
可得从抛出到$B$点的时间为$t_{B}=\dfrac{y_{1}+y_{2}}{2g}\sqrt{\dfrac{g}{y_{2}-y_{1}}}$
抛出点的横坐标为$x=- (v_{0}t_{B}-x_{0})=\dfrac{y_{2}-3y_{1}}{2(y_{2}-y_{1})}x_{0}$
抛出点的纵坐标为$y=- (\dfrac{1}{2}gt_{B}^{2}-y_{1})=\dfrac{- 9y_{1}^{2}+6y_{2}y_{2}-y_{2}^{2}}{8(y_{2}-y_{1})}$
高中 | 探究平抛运动的特点题目答案及解析(完整版)
