高中 | 探究平抛运动的特点 题目答案及解析
稿件来源:高途
高中 | 探究平抛运动的特点题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.3 实验:研究平抛运动
探究平抛运动的特点
实验小组用如图甲所示的装置,来探究斜面对平抛运动的制约性,$B$点是$A$点在水平地面的投影点,$AC$是固定在轨道与地面之间的斜面,小球在水平桌面上获得水平向右的速度,然后在$A$点以水平向右的初速度$v_{0}$(可通过安装在$A$的光电门测出)做平抛运动,落到$AC$或$CD$平面上,用刻度尺测出小球的落点与$AB$之间的距离为$x$,多次做实验,获取数据,画出的$v_{0}^{2}-x$关系图像如图乙所示,画出的$v_{0}-x$关系图像如图丙所示,重力加速度为$g$,设$∠BAC=\theta$,回答下列问题。
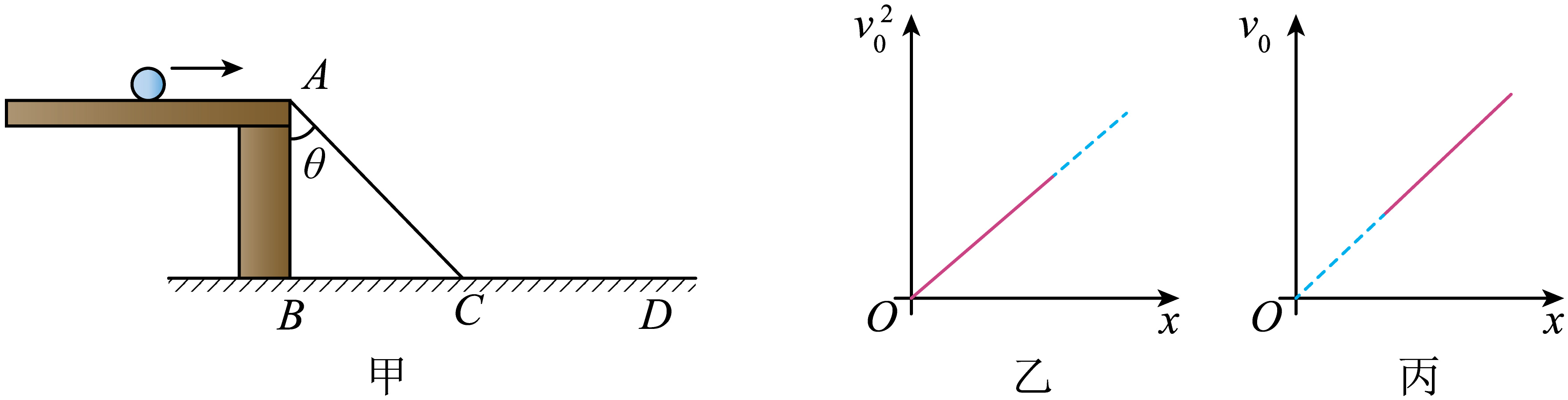
图 (选填“乙”或“丙”)说明小球落在水平面$CD$上,图 (选填“乙”或“丙”)说明小球落在斜面$AC$上;
若小球落在斜面$AC$上,由平抛运动知识$x=v_{0}t$,$y=\dfrac{1}{2}gt^{2}$,$\dfrac{x}{y}=\tan\theta$
综合可得$v_{0}^{2}=\dfrac{g\tan\theta}{2}x$
说明$v_{0}^{2} − x$图像是过原点的一条倾斜的直线,对应的图像为图乙,图像的斜率$k=\dfrac{g\tan\theta}{2}$
若小球落到水平面$CD$上,平抛运动高度不变,运动时间$t$不变,则有$v_{0}-\dfrac{1}{t}x$
则$v_{0} − x$关系图像是过原点的一条倾斜直线,对应的图像为图丙,即图丙说明小球落在水平面$CD$上,图乙说明小球落在斜面$AC$上。
图丙对应小球平抛运动的时间 (选填“是”或“不是”)定值,若图丙的斜率为$k_{1}$,则$A$、$B$两点的高度差为 ;
图丙对应小球平抛运动的时间$t= \dfrac{x}{v_{0}}$是定值,若图丙的斜率为$k_{1}$,则有$k_{1}=\dfrac{1}{t}$
可得$t=\dfrac{1}{k_{1}}$
所以$A$、$B$两点的高度差为$h=\dfrac{1}{2}gt^{2}=\dfrac{g}{2k_{1}^{2}}$
若图乙的斜率为$k_{2}$,则$\theta$的正切值为 。
若图乙的斜率为$k_{2}$,则$k_{2}=\dfrac{g\tan\theta}{2}$
解得$\tan\theta=\dfrac{2k_{2}}{g}$
高中 | 探究平抛运动的特点题目答案及解析(完整版)
