如图所示，图甲为磁流体发电机原理示意图，图乙为质谱仪原理图，图丙是宽为$a$，长为$c$的半导体霍尔元件，元件内的导电粒子是电荷量为$e$的自由电子，图丁是速度选择器的原理示意图，不计粒子的重力，下列说法正确的是$(\qquad)$

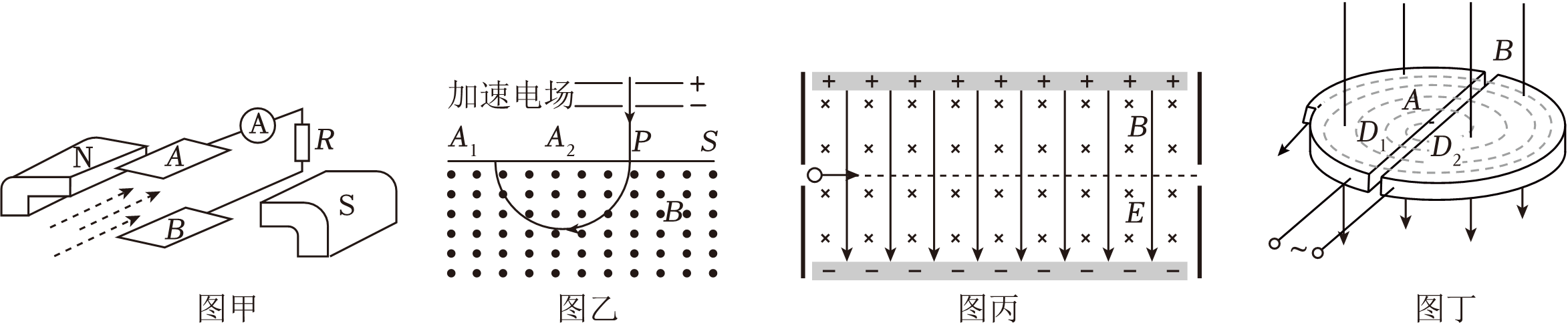
图甲为磁流体发电机原理示意图，将一束等离子体喷入磁场，$A$、$B$板间产生电势差，$A$板电势高

图乙为质谱仪原理图，$ \\rm _{1}^{1}H$、$ \\rm _{1}^{2}H$、$\\rm _{1}^{3}H$三种粒子经加速电场射入磁场，$ \\rm _{1}^{3}H$在磁场中的偏转半径最大

图丙为速度选择器，带电粒子（不计重力）能够从右向左沿图中虚线匀速运动

图丁为回旋加速器的原理示意图，忽略粒子在图丁的$D$形盒狭缝中的加速时间，随着粒子速度的增大，交变电流的频率也应该增大

$\rm A$．图甲中，将一束等离子体喷入磁场，根据左手定则可知，带正电的离子向$B$板偏转，则$B$板电势高，故$\rm A$错误；

$\rm B$．图乙中，$\rm _{1}^{1}H$、$ \rm _{1}^{2}H$、$ \rm _{1}^{3}H$三种粒子经加速电场射入磁场，设加速电场的电压为$U$，根据动能定理可得：$qU = \dfrac{1}{2}mv^{2}$

在磁场中，洛伦兹力提供向心力，根据牛顿第二定律可得：$Bqv = m\dfrac{v^{2}}{r}$

解得：$r = \dfrac{1}{B}\sqrt{\dfrac{2mU}{q}}$

$\rm _{1}^{3}H$粒子的比荷最小，则$ _{1}^{3}H$在磁场中的偏转半径最大，故$\rm B$正确；

$\rm C$．粒子从左边水平进入时能匀速直线通过，是因为洛伦兹力与电场力等大反向，合力为零。若从右边进入，则受到的电场力与洛伦兹力同向，合力不为零，则无法匀速直线通过，故$\rm C$错误；

$\rm D$．回旋加速器正常工作时，忽略粒子在图丁的$D$形盒狭缝中的加速时间，交流电流的周期等于粒子做圆周运动的周期，其周期为$T = \dfrac{2\pi m}{qB}$

周期与速度大小无关，保持不变，所以随着粒子速度的增大，交变电流的周期不变，频率也不变，故$\rm D$错误。

故选：$\rm B$。