高中 | 胡克定律 题目答案及解析
稿件来源:高途
高中 | 胡克定律题目答案及解析如下,仅供参考!
必修1
第三章 相互作用
3.2 弹力
胡克定律
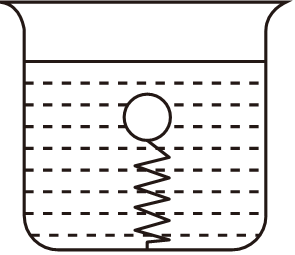
如图所示,小球密度小于烧杯中水的密度,球固定在弹簧上,弹簧下端固定在杯底。当装置静止时,弹簧伸长$\Delta x$,当整个装置在自由下落的过程中弹簧的伸长将$(\qquad)$
["
仍为$\\Delta x$
","大于$\\Delta x$
","小于$\\Delta x$
","等于零
"][["D"]]
小球静止时受重力、浮力和弹簧的拉力处于平衡,当自由下落时,处于完全失重状态,系统的加速度为$g$,则最终弹簧的拉力为零,形变量为零,故$\rm D$正确,$\rm ABC$错误。
故选:$\rm D$。
高中 | 胡克定律题目答案及解析(完整版)
去刷题
相关题库:
如图所示,挡板固定在倾角为的斜面左下端,斜面右上端与半径为的圆弧轨道连接,其圆心在斜面的延长线上。点有一光滑轻质小滑轮,。质量均为的小物块、由一轻质弹簧拴接(弹簧平行于斜面),其中物块紧靠在挡板处,物块用跨过滑轮的轻质细绳与一质量为、大小可忽略的小球相连,初始时刻小球锁定在点,细绳与斜面平行,且恰好绷直而无张力,、处于静止状态。某时刻解除对小球的锁定,当小球沿圆弧运动到最低点时(物块未到达点),物块对挡板的作用力恰好为。已知重力加速度为,不计一切摩擦,下列说法正确的是
如图甲所示,倾角为的足够长的光滑斜面体放置在光滑水平面上,上端有垂直斜面的挡板,与斜面平行的轻弹簧上端固定在挡板上,下端连接质量为的物块(可视为质点)。现对斜面体施加一水平向右的推力,测得推力的大小随弹簧的形变量的变化规律如图乙所示(取弹簧伸长为正,压缩为负)。若弹簧始终在弹性限度内,重力加速度,,,则斜面体的质量和轻弹簧的劲度系数分别为
如图甲所示,轻弹簧竖直固定在水平面上,一质量为的小球,从弹簧上端某高度处自由下落(空气阻力可忽略),从它接触弹簧到弹簧压缩至最短的过程中(弹簧始终在弹性限度内),其速度和弹簧压缩量间的函数图像如图乙所示,其中为曲线的最高点,小球和弹簧接触瞬间机械能损失不计,取,则下列说法正确的是
某同学有三个小球、、,其中、小球的质量均为,小球的质量未知。他先将小球、穿在光滑的水平细杆上,中间通过原长为的轻弹簧相连,然后通过长度均为的轻绳,分别与球相连,如图所示,三球稳定后,均处于静止状态,此时两轻绳间的夹角恰为。该同学想利用三球之间力的关系算出球的质量,计算过程中发现弹簧劲度系数未知,于是想要根据胡克定律测出该弹簧的劲度系数,他设计了如图所示的装置测量弹簧的劲度系数,先将刻度尺(刻度在上端)竖直立在桌腿边缘靠近弹簧的位置,当只挂小球时,弹簧的指针指在刻度处,当同时挂小球、时,弹簧的指针指在刻度处。整个过程弹簧始终在弹性限度内,重力加速度为,求:
如图所示,物块放在台式测力计上,通过跨过定滑轮的轻绳与物块相连,下端与一轻质弹簧相连,弹簧的下端与地面接触(未拴接),整个系统处于平衡状态,此时台式测力计的示数为;已知,物块、间的水平距离,倾斜绳与水平方向的夹角(滑轮右侧绳竖直),物块与台式测力计间动摩擦因数,最大静摩擦力等于滑动摩擦力,、和滑轮视为质点,不计滑轮质量和滑轮处摩擦,弹簧一直在弹性限度内,取(已知,,)。
物理学中,有很多描述物体、物质的性质或者“本领”的物理量。
今日推荐 ![]()
![]()
![]()
