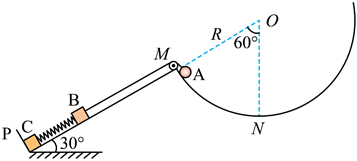
如图所示，挡板$P$固定在倾角为$30{}^\circ $的斜面左下端，斜面右上端$M$与半径为$R$的圆弧轨道$MN$连接，其圆心$O$在斜面的延长线上。$M$点有一光滑轻质小滑轮，$\angle MON=60{}^\circ $。质量均为$m$的小物块$B$、$C$由一轻质弹簧拴接（弹簧平行于斜面），其中物块$C$紧靠在挡板$P$处，物块$B$用跨过滑轮的轻质细绳与一质量为$4m$、大小可忽略的小球$A$相连，初始时刻小球$A$锁定在$M$点，细绳与斜面平行，且恰好绷直而无张力，$B$、$C$处于静止状态。某时刻解除对小球$A$的锁定，当小球$A$沿圆弧运动到最低点$N$时（物块$B$未到达$M$点），物块$C$对挡板的作用力恰好为$0$。已知重力加速度为$g$，不计一切摩擦，下列说法正确的是$(\qquad)$

弹簧的劲度系数为$\\dfrac{2mg}{R}$

小球$A$到达$N$点时的速度大小为$\\sqrt{\\dfrac{12}{19}gR}$

小球$A$到达$N$点时的速度大小为$\\sqrt{\\dfrac{8}{15}gR}$

小球$A$由$M$运动到$N$的过程中，小球$A$和物块$B$的机械能之和一直在增大

$\text{A}$、设弹簧的劲度系数为$k$，初始时刻弹簧的压缩长度为${{x}_{1}}$，则$B$沿斜面方向受力平衡，则$mg\sin 30{}^\circ =k{{x}_{1}}$，小球$A$沿圆弧运动到最低点$N$时，物块$C$即将离开挡板时，设弹簧的拉伸长度为${{x}_{2}}$，则$C$沿斜面方向受力平衡，则$mg\sin 30{}^\circ =k{{x}_{2}}$，由几何知识可知，此时细线的长度变化为${{x}_{1}}+{{x}_{2}}=MN=R$，解得$k=\dfrac{mg}{R}$，故$\text{A}$错误；

$\text{BC}$、设小球$A$到达$N$点时的速度为$v$，对$v$进行分解，在沿绳子方向的速度$v'=v\cos 30{}^\circ $，由于沿绳子方向的速度处处相等，所以此时$B$的速度也为$v'$，对$A$、$B$、$C$和弹簧组成的系统，在整个过程中，只有重力和弹簧弹力做功，且$A$在$M$和$N$处，弹簧的形变量相同，故弹性势能不变，弹簧弹力做功为$0$，重力对$A$做正功，对$B$做负功，$A$、$B$、$C$和弹簧组成的系统机械能守恒，可知$4mgR(1-\cos 60{}^\circ )-mg({{x}_{1}}+{{x}_{2}})\sin 30{}^\circ =\dfrac{1}{2}4m{{v}^{2}}+\dfrac{1}{2}mv{{'}^{2}}$，解得$v=\sqrt{\dfrac{12}{19}gR}$，故$\text{B}$正确，$\text{C}$错误；

$\text{D}$、小球$A$由$M$运动到$N$的过程中，$A$、$B$、$C$和弹簧组成的系统机械能守恒，则小球$A$和物块$B$的机械能之和与弹簧和$C$的能量之和不变，$C$一直处于静止状态，弹簧一开始处于压缩状态，之后变为原长，后开始拉伸，则弹性势能先减小受增大，故小球$A$和物块$B$的机械能之和先增大后减小，故$\text{D}$错误。

故选：$\text{B}$。