高中 | 受力分析 题目答案及解析
稿件来源:高途
高中 | 受力分析题目答案及解析如下,仅供参考!
必修1
第三章 相互作用
3.5 力的分解
受力分析
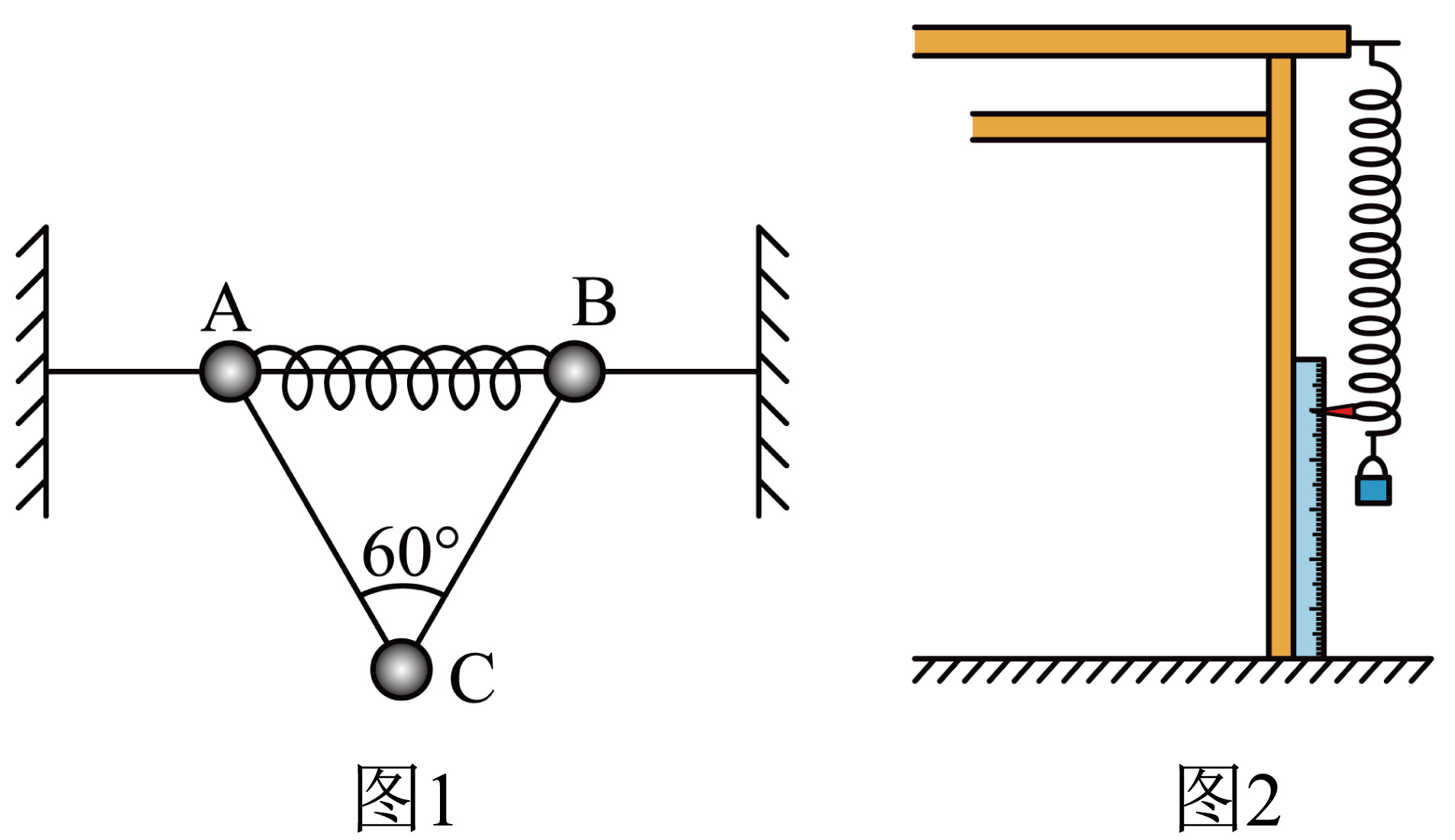
某同学有三个小球$A$、$B$、$C$,其中$A$、$B$小球的质量均为$m$,$C$小球的质量未知。他先将小球$A$、$B$穿在光滑的水平细杆上,中间通过原长为$1.2l$的轻弹簧相连,然后通过长度均为$l$的轻绳,分别与$C$球相连,如图$1$所示,三球稳定后,均处于静止状态,此时两轻绳间的夹角恰为$60^\circ$。该同学想利用三球之间力的关系算出$C$球的质量,计算过程中发现弹簧劲度系数未知,于是想要根据胡克定律测出该弹簧的劲度系数,他设计了如图$2$所示的装置测量弹簧的劲度系数,先将刻度尺($0$刻度在上端)竖直立在桌腿边缘靠近弹簧的位置,当只挂小球$A$时,弹簧的指针指在$l_{1}$刻度处,当同时挂小球$A$、$B$时,弹簧的指针指在$l_{2}$刻度处。整个过程弹簧始终在弹性限度内,重力加速度为$g$,求:
轻弹簧的劲度系数;
$k=\\dfrac{mg}{l_{2}- l_{1}}$
"]]设挂在桌边的轻弹簧未挂小球时,弹簧的指针指在$l_{0}$处,根据胡克定律可知,当挂上质量为$m$的小球$A$时,有$mg=k(l_{1}-l_{0})$
当把$A$、$B$球同时挂上时,有$2mg=k(l_{2}-l_{0})$
两式联立可得弹簧的劲度系数$k=\dfrac{mg}{l_{2}-l_{1}}$
小球$C$的质量。
$M= \\dfrac{2\\sqrt{3}l}{5\\left( l_{2}-l_{1} \\right)}m$
"]]设小球$C$的质量为$M$,细绳上的拉力为$T$,对小球$C$分析受力,有$2T\cos 30^\circ =Mg$
解得$T=\dfrac{\sqrt{3}}{3}Mg$
对小球$A$分析受力有$k(1.2l-l)=T\cos 60^\circ $
代入数据解得$M=\dfrac{2\sqrt{3}l}{5\left( l_{2}-l_{1} \right)}m$
高中 | 受力分析题目答案及解析(完整版)
