如图所示，在一个场强大小为$E=$$\dfrac{\sqrt{3}mg}{3q}$的区域内有一个倾角为$60^\circ$的斜面，当场强方向水平向右时，在高为$h$的斜面顶端一个质量为$m$带电量为$q$的带电物体能静止在其上。某时刻场强方向突然换成水平向左,其大小不变,最后物体运动到水平面上。则场强未变向时物体所受的摩擦力和物体刚与水平地面接触时的速度大小分别为$(\qquad)$

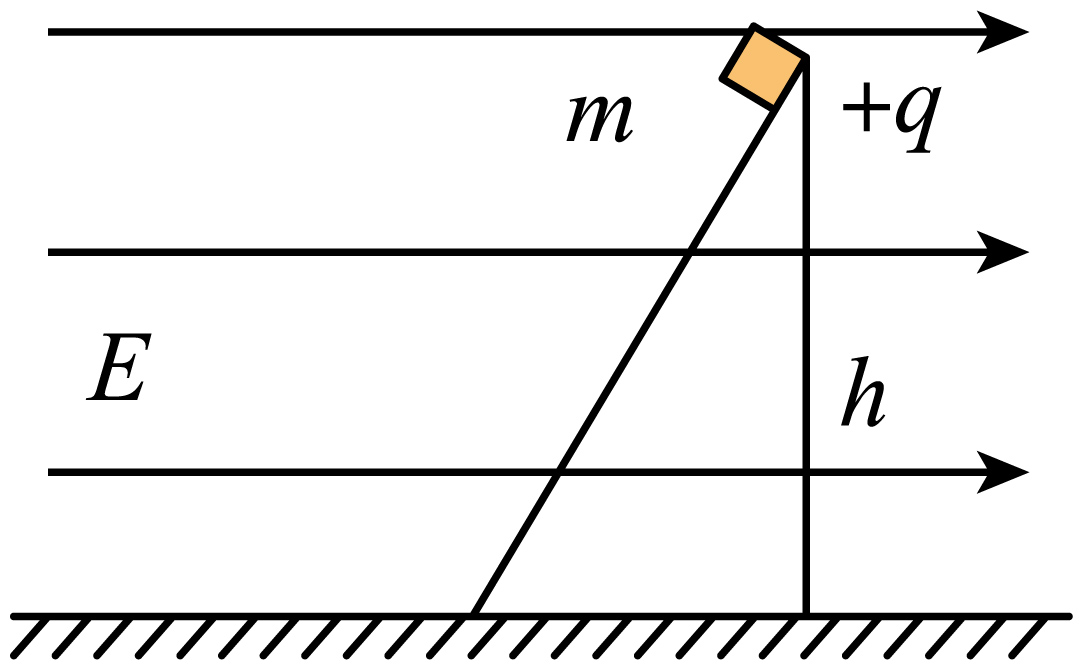
$\\dfrac{2mg}{3}$，$\\dfrac{\\sqrt{2gh}}{2}$

$\\dfrac{2}{3}mg$，$2\\sqrt{gh}$

$\\dfrac{\\sqrt{3}}{3}mg$，$\\dfrac{2\\sqrt{6gh}}{3}$

$\\dfrac{\\sqrt{3}}{3}mg$，$2\\sqrt{gh}$

场强未变向时，对物体受力分析如图所示：

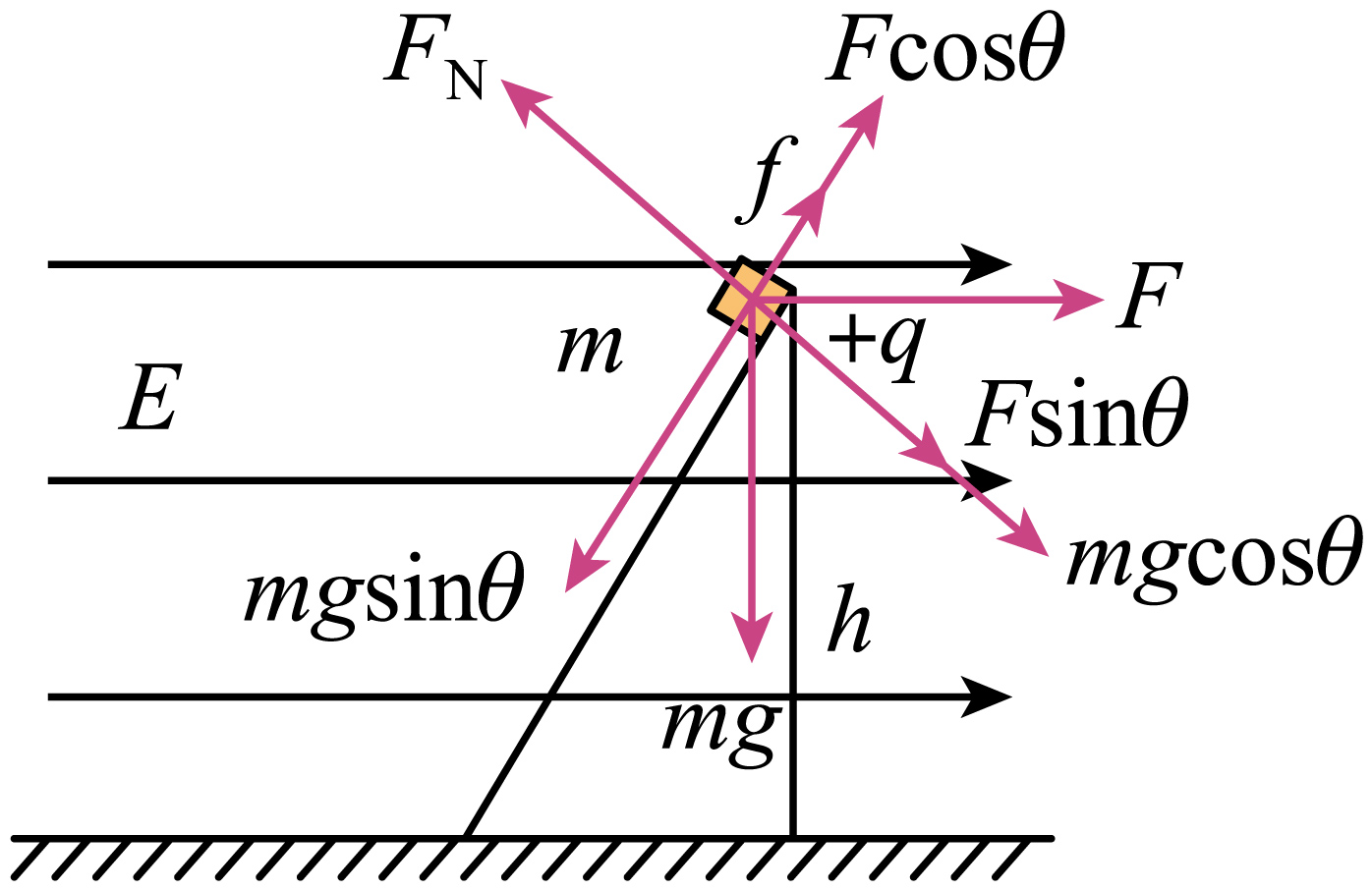
根据平衡条件得：$mg\sin \theta=F\cos \theta+f$，其中$F=qE=\dfrac{\sqrt{3}}{3}mg$，解得：$f=\dfrac{\sqrt{3}}{3}mg$；

场强方向改变时，受力分析如图

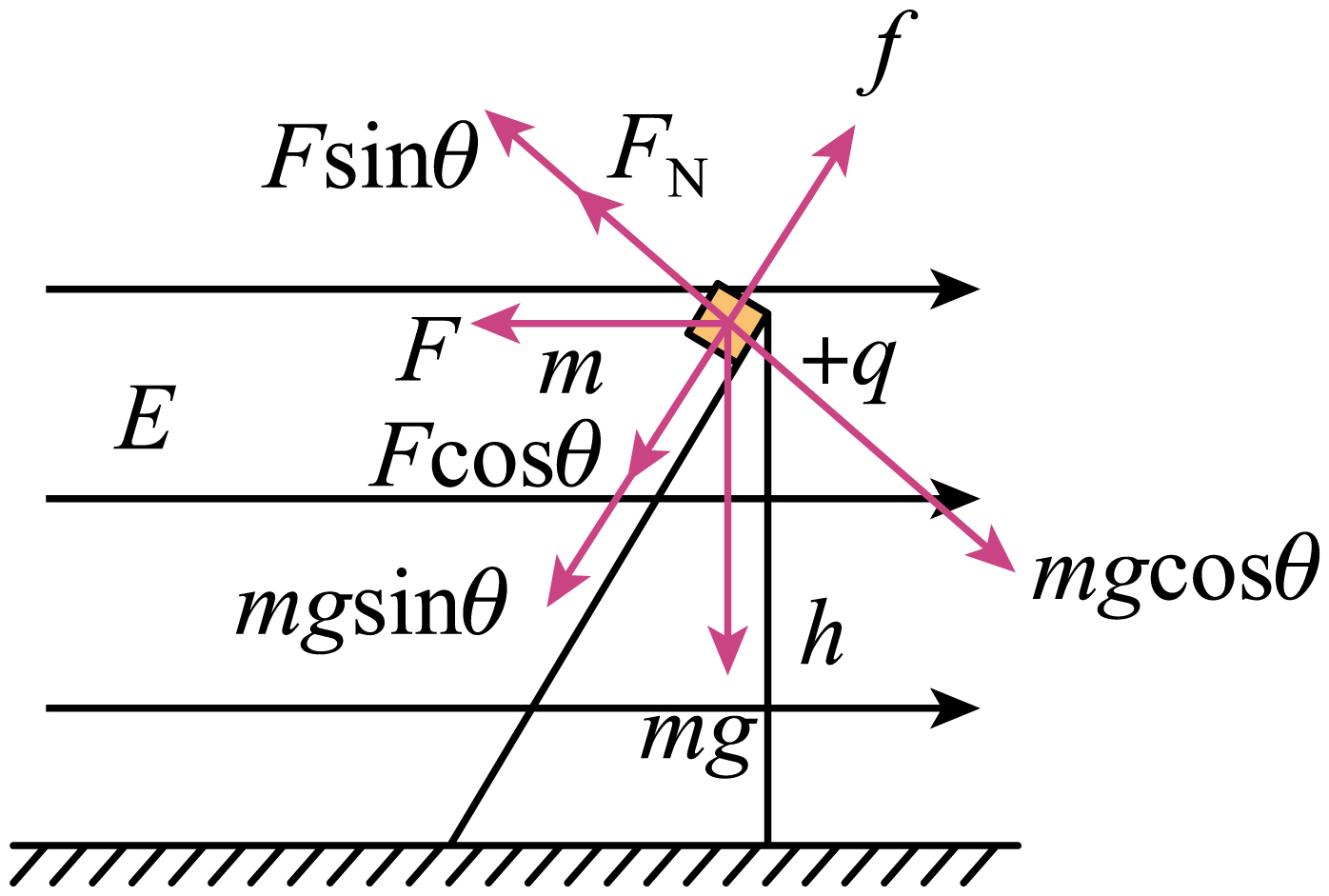
因为$F\sin\theta=\dfrac{1}{2}mg=mg\cos\theta=\dfrac{1}{2}mg$， 故$F_{N}=0$，摩擦力$f=0$，

故物体只受电场力和重力作用，则合力为$F_{合}=\sqrt{F^{2}+(mg)^{2}}=\dfrac{2\sqrt{3}}{3}mg$，

则加速度为$a=\dfrac{F_{合}}{m}=\dfrac{2\sqrt{3}}{3}g$，根据速度位移公式得：$v^{2}=2a \cdot \dfrac{h}{\sin\theta}$，

解得：$v=\sqrt{2a \cdot \dfrac{h}{\sin\theta}}=\dfrac{2\sqrt{6gh}}{3}$。

故选：$\rm C$$.$