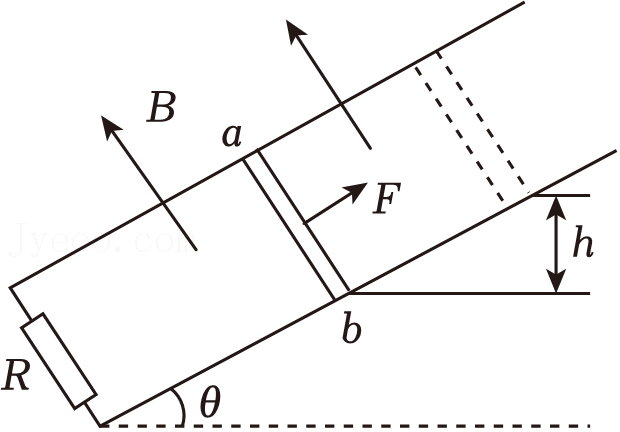
两根光滑的金属导轨，平行放置在倾角为$\theta$的斜面上，导轨的左端接有电阻$R$，导轨自身的电阻可忽略不计，斜面处在一匀强磁场中，磁场方向垂直于斜面向上，质量为$m$、电阻为$r$的金属棒$ab$，在沿着斜面与棒垂直的恒力$F$作用下沿导轨匀速上滑，并上升$h$高度，如图所示。在这过程中$(\qquad)$

作用于金属棒上的各个力的合力所做的功等于$mgh$与电阻$R$上产生的焦耳热之和

金属棒克服安培力做的功等于电阻$R$和$r$上产生的焦耳热之和

恒力$F$与重力的合力所做的功等于电阻$R$上产生的焦耳热

作用于金属棒上的各个力的合力所做的功等于零

$\rm AD$、金属棒沿导轨匀速上滑，金属棒受重力、安培力和恒力$F$作用，由动能定理有：$W_{合}=W_{F}+W_{G}+W_{A}=\Delta E_{k}=0$

即作用于金属棒上的各个力的合力所做的功等于零，故$\rm A$错误，$\rm D$正确；

$\rm B$、由于导轨自身的电阻可忽略不计，则根据功能关系可知，金属棒克服安培力做的功等于电阻$R$和$r$上产生的焦耳热之和，故$\rm B$正确；

$\rm C$、由$AD$分析可知，恒力$F$与重力的合力所做的功等于金属棒克服安培力做的功，则恒力$F$与重力的合力所做的功等于电阻$R$和$r$上产生的焦耳热之和，故$\rm C$错误。

故选：$\rm BD$。