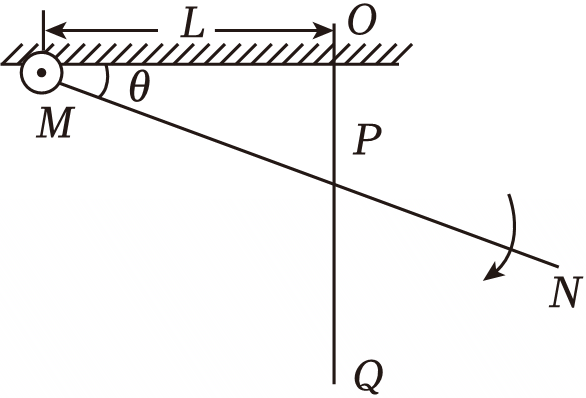
如图所示，$MN$杆绕$M$点在竖直平面内匀速转动，并带动套在固定光滑竖直杆$OQ$上的小环向下运动，某一时刻小环运动到$P$点时速度正好为$v$，$∠OMP=\theta$。已知$OM=L$，则$MN$杆的角速度大小为$(\qquad)$

$\\dfrac{v\\cos^{2}\\theta}{L}$

$\\dfrac{v\\cos\\theta}{L}$

$\\dfrac{v\\cos\\theta \\sin\\theta}{L}$

$\\dfrac{v\\sin^{2}\\theta}{L}$

设$MN$杆的角速度为$\omega$，如图所示

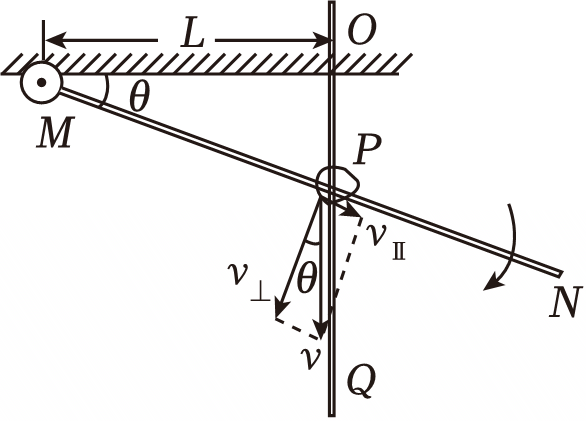
把速度$v$沿着$MN$杆和垂直$MN$杆分解如图所示，则$v_{⊥}=v\cos\theta$

根据$v=r\omega$得：$v_{⊥}=\omega\times MP$

根据几何关系得：$MP=\dfrac{L}{\cos\theta}$

联立解得：$\omega=\dfrac{v\cos^{2}\theta}{L}$

故$\rm A$正确，$\rm BCD$错误。

故选：$\rm A$。