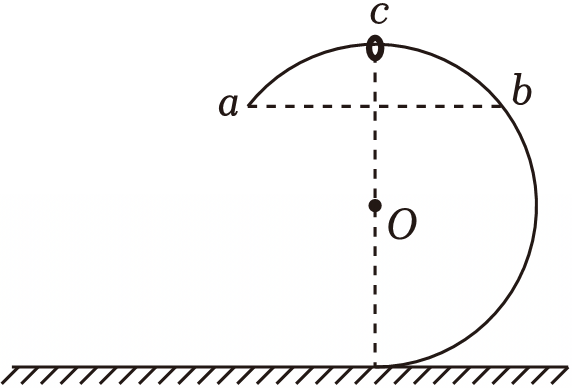
如图所示，一半径为$R$的光滑大圆环竖直固定在水平面上，其上套一小环，$a$、$b$为圆环上关于竖直直径对称的两点，将$a$点下方圆环拆走，若小环从大圆环的最高点$c$由静止开始下滑，当小环滑到$b$点时，恰好对大圆环无作用力。已知重力加速度大小为$g$，若让小环从最高点$c$由静止下滑从$a$点滑离，小环滑离$a$点时竖直分速度大小为$(\qquad)$

$\\dfrac{1}{3}\\sqrt{\\dfrac{10gR}{3}}$

$\\sqrt{\\dfrac{2gR}{3}}$

$\\dfrac{2}{3}\\sqrt{\\dfrac{2gR}{3}}$

$\\dfrac{2}{3}\\sqrt{gR}$

设$b$点与$O$点的连线与竖直方向的夹角为$\theta$，如图所示。

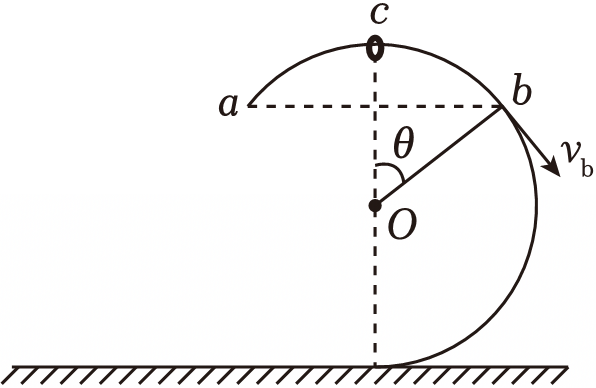
从$c$到$b$，由动能定理得$mgR(1-\cos\theta)=\dfrac{1}{2}mv_{b}^{2}$

小环滑到$b$点时，由重力沿半径方向的分力提供向心力，由牛顿第二定律得$mg\cos\theta=m\dfrac{v_{b}^{2}}{R}$

解得$\cos\theta=\dfrac{2}{3}$，$v_{b}=\sqrt{\dfrac{2}{3}gR}$

由对称性可知，小环滑离$a$点时的速度为$v_{a}=v_{b}=\sqrt{\dfrac{2}{3}gR}$

小环滑离$a$点时竖直分速度大小为$v_{ay}=v_{a}\sin\theta=\sqrt{\dfrac{2}{3}gR} \times \dfrac{\sqrt{5}}{3}=\dfrac{1}{3}\sqrt{\dfrac{10gR}{3}}$，故$\rm A$正确，$\rm BCD$错误。

故选：$\rm A$。