如图所示，物块$A$用不可伸长的轻绳绕过轻质光滑定滑轮与置于光滑水平面上的物块$B$连接，物块$A$、$B$的质量均为$m$，施加外力使物块$A$、$B$保持静止，此时轻绳恰好处于伸直状态。某时刻撤去外力，两物块同时由静止开始运动，当物块$A$下落高度为$h$时，其加速度大小为$a$，方向竖直向下，此时连接物块$B$的轻绳与水平方向的夹角为$\theta$，整个过程物块$B$始终未离开水平面，已知重力加速度为$g$。当物块$A$下落高度为$h$时，下列说法正确的是$(\qquad)$

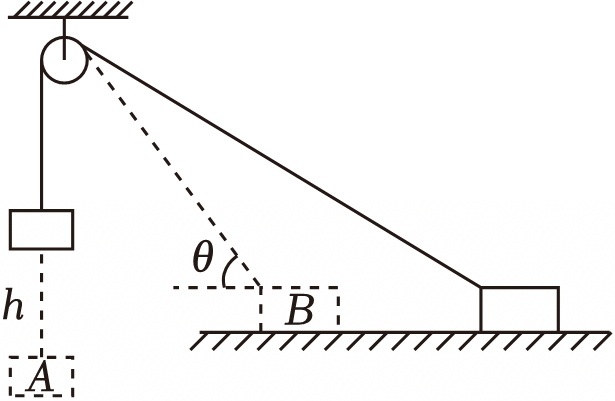
物块$B$的加速度大小为$\\dfrac{a}{\\cos\\theta}$

物块$B$的加速度大小为$(g+a)\\cos\\theta$

物块$A$的速度大小为$\\sqrt{\\dfrac{2gh}{1+\\cos^{2}\\theta}}$

物块$A$的速度大小为$\\sqrt{\\dfrac{2gh\\cos^{2}\\theta}{1+\\cos^{2}\\theta}}$

$\rm AB$、对物块$A$由牛顿第二定律得：$mg-T=ma$

对物块$B$由牛顿第二定律得：$T\cos\theta=ma_{B}$

联立解得物块$B$的加速度大小为：$a_{B}=(g-a)\cos\theta$，故$\rm AB$错误；

$\rm CD$、对物块$A$和$B$整体，根据机械能守恒定律的：$mgh=\dfrac{1}{2}mv_{A}^{2}+\dfrac{1}{2}mv_{B}^{2}$

$A$、$B$的速度的关联如下图所示，可得$A$、$B$的速度大小关系为：$v_{A}=v_{B}\cos\theta$

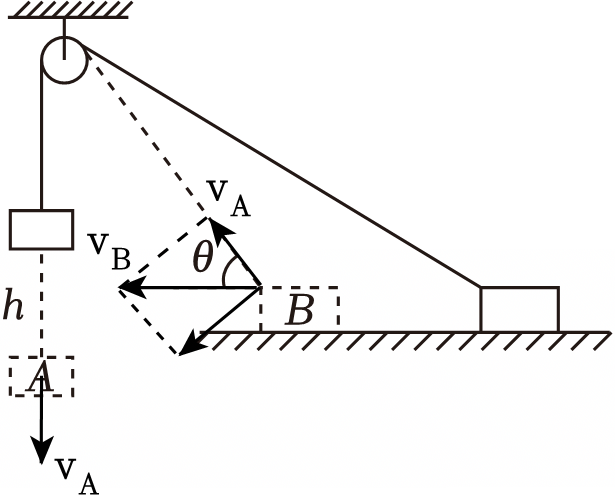
联立解得：$v_{A}=\sqrt{\dfrac{2gh\cos^{2}\theta}{1+\cos^{2}\theta}}$，故$\rm C$错误，$\rm D$正确。

故选：$\rm D$。