$2021$年$11$月，中科院国家天文台发布了目前世界上最大时域多星光谱星表，为科学家研究宇宙中的多星系统提供了关键数据支持。科学家观测到有三颗星$A$、$B$、$C$保持相对静止，相互之间的距离均为$l$，且一起绕着某点做周期为$T$的匀速圆周运动。已知$m_{A}=m$，$m_{B}=m_{C}=(\sqrt{3}+1)m$，不计其它星体对它们的影响。关于这个三星系统，下列说法正确的是$(\qquad)$

三颗星$A$、$B$、$C$的半径之比为$1:1:1$

三颗星$A$、$B$、$C$的线速度大小之比为$\\sqrt{2}:1:1$

若距离$l$均不变，$A$、$B$、$C$的质量均变为原来的$2$倍，则周期变为$\\dfrac{1}{2}T$

若$A$、$B$、$C$的质量不变，距离均变为$2l$，则周期变为$\\sqrt{2}T$

$\rm A$．三星角速度与周期相等，根据对称性，$B$、$C$轨道半径相等，如图所示

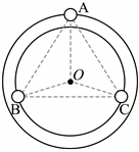
对$A$星体有：$2G\dfrac{(\sqrt{3}+1)m^{2}}{l^{2}}\cos30{^\circ}=m\omega^{2}R_{A}$，对$B$、$C$星体，两星体各自所受引力的合力大小相等，令为$F$，根据余弦定理有$F^{2}={\left\lbrack G\dfrac{(\sqrt{3}+1)m^{2}}{l^{2}}\right\rbrack}^{2}+{\left\lbrack G\dfrac{{(\sqrt{3}+1)}^{2}m^{2}}{l^{2}}\right\rbrack}^{2}-2G\dfrac{(\sqrt{3}+1)m^{2}}{l^{2}} \cdot G\dfrac{{(\sqrt{3}+1)}^{2}m^{2}}{l^{2}}\cos120{^\circ}$

$B$、$C$轨道半径相等，令为$R_{B}=R_{C}=R_{0}$，则有：$F=(\sqrt{3}+1)m\omega^{2}R_{0}$，解得$\dfrac{R_{A}}{R_{0}}=\sqrt{2}$，则三颗星的半径大小之比为$\sqrt{2}:1:1$，故$\rm A$错误；

$\rm B$．根据线速度与角速度的关系有：$v=\omega R$，三颗星的线速度之比等于$\sqrt{2}:1:1$，故$\rm B$正确；

$\rm C$．距离$l$均不变，对$A$星体有：$2G\dfrac{(\sqrt{3}+1)m^{2}}{l^{2}}\cos30{^\circ}=m\dfrac{4\pi^{2}}{T^{2}}R_{A}$，若$A$、$B$、$C$的质量均变为原来的$2$倍，根据对称性可知，三星圆周运动的圆心不变，即轨道半径不变，则有$2G\dfrac{4 \times (\sqrt{3}+1)m^{2}}{l^{2}}\cos30{^\circ}=2m\dfrac{4\pi^{2}}{T_{1}^{2}}R_{A}$，解得$T_{1}=\dfrac{\sqrt{2}T}{2}$，即若距离$l$均不变，$A$、$B$、$C$的质量均变为原来的$2$倍，则周期变为$\dfrac{\sqrt{2}}{2}T$，故$\rm C$错误；

$\rm D$．若$A$、$B$、$C$的质量不变，距离均变为$2l$，根据对称性可知，三星圆周运动的圆心不变，即轨道半径均变为先前的$2$倍，则对$A$星有：$2G\dfrac{(\sqrt{3}+1)m^{2}}{{(2l)}^{2}}\cos30{^\circ}=m\dfrac{4\pi^{2}}{T_{2}^{2}} \cdot 2R_{A}$

解得$T_{2}=2\sqrt{2}T$，即若$A$、$B$、$C$的质量不变，距离均变为$2l$，则周期变为$2\sqrt{2}T$，故$\rm D$错误。

故选：$\rm B$。