如图所示，劲度系数为$k$的轻质弹簧一端固定在竖直墙壁上，另一端与质量为$m$的小滑块$A$相连接，在$A$的右边靠着另一质量为$m$的滑块$B$，$A$与$B$不粘连。已知$A$、$B$与水平地面的动摩擦因数均为$\mu $，且最大静摩擦力等于滑动摩擦力。已知弹簧的弹性势能$E_{\text{p}}=\dfrac{1}{2}kx^{2}$，其中$k$为弹簧的劲度系数，$x$为弹簧的形变量。现将$A$、$B$一起由原长$O$处向左压缩弹簧，当压缩量$x_{0}=\dfrac{2\left( 1+\sqrt{5} \right)\mu mg}{k}$时将滑块$A$、$B$由静止释放，则在$A$、$B$以后的运动过程中，下列说法正确的是$(\qquad)$

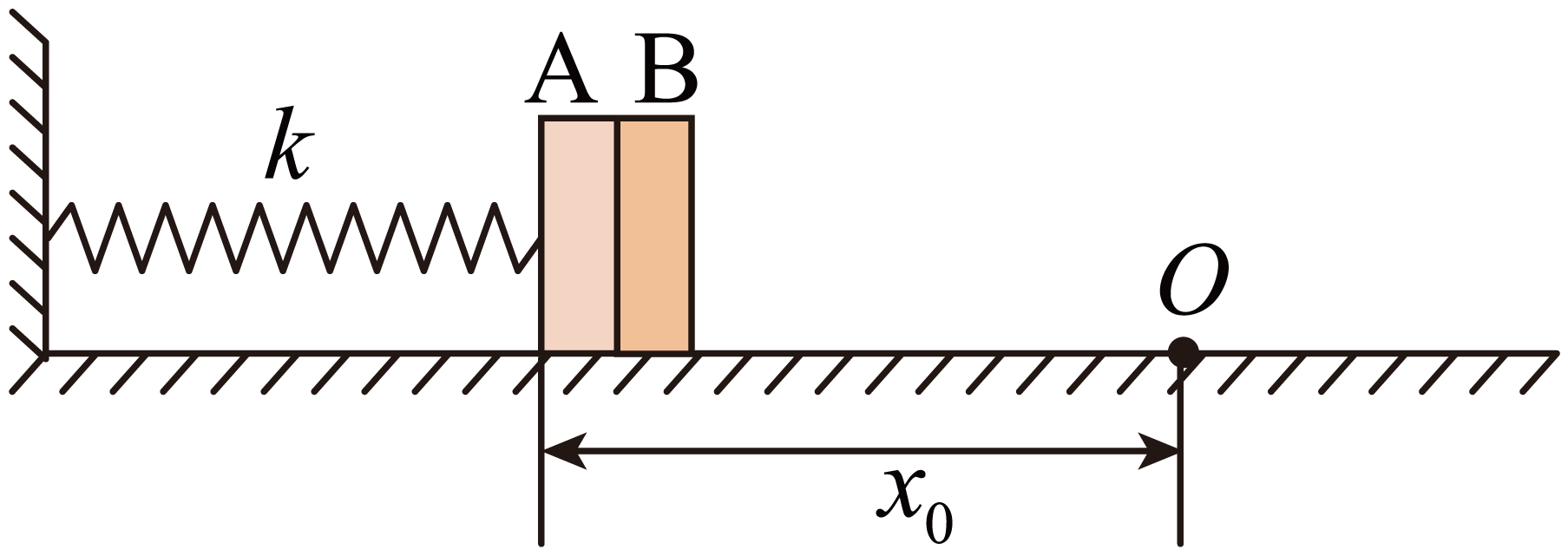
滑块$A$、$B$将在$O$点右侧分离

滑块$B$运动的总位移大小为$\\dfrac{2\\left( 3+\\sqrt{5} \\right)\\mu mg}{k}$

$A$向右运动的最大位移为$\\dfrac{2\\left( 3+\\sqrt{5} \\right)\\mu mg}{k}$

当$A$、$B$都静止时$A$与$B$间的距离为$\\dfrac{4\\mu mg}{k}$

$\rm A$．将滑块$A$、$B$由静止释放，两滑块水平方向上受到弹簧的弹力和滑动摩擦力，滑动摩擦力不变，而弹簧的弹力随着压缩量的减小而减小，弹力先大于滑动摩擦力，后小于滑动摩擦力，则两滑块向右先做加速运动后做减速运动。经分析可知两滑块分离时应发生在减速阶段，分离时两滑块的弹力为零，对滑块$B$有$a_{\text{B}}=\dfrac{\mu mg}{m}=\mu g$

对滑块$A$有$a_{\text{A}}=\dfrac{\mu mg+F_{弹}}{m}=\mu g+\dfrac{F_{弹}}{m}$

恰好分离时有$a_{A}=a_{B}$

解得$F_{弹}=0$

说明两滑块在将在弹簧原长处，即$O$点分离，选项$\rm A$错误；

$\rm B$．设两滑块分离时的速度为$v_{0}$，根据能量守恒有$\dfrac{1}{2}k{x_{0}}^{2}=\mu \times 2mg \times x_{0}+\dfrac{1}{2} \times 2m \times {v_{0}}^{2}$

又$x_{0}=\dfrac{2\left( 1+\sqrt{5} \right)\mu mg}{k}$

解得${v_{0}}^{2}=\dfrac{8m\mu^{2}g^{2}}{k}$

分离后滑块$B$做匀减速运动直到停止，设此过程的位移为$x_{B}$，则有$x_{\text{B}}=\dfrac{{v_{0}}^{2}}{2a_{\text{B}}}=\dfrac{4\mu mg}{k}$

则滑块$B$运动的总位移大小为$x_{\text{B}总}=x_{\text{B}}+x_{0}=\dfrac{2(3+\sqrt{5})\mu mg}{k}$

选项$\rm B$正确；

$\rm C$．分离后滑块$A$做减速度运动，向右运动的最大位移时速度为$0$，设此过程的位移为$x_{A}$，根据能量守恒有$\dfrac{1}{2}m{v_{0}}^{2}=\mu mgx_{\text{A}}+\dfrac{1}{2}k{x_{\text{A}}}^{2}$

解得$x_{\text{A}}=\dfrac{2\mu mg}{k}$

则$A$向右运动的最大位移为$x_{\text{A}总}=x_{\text{A}}+x_{0}=\dfrac{2(2+\sqrt{5})\mu mg}{k}$

选项$\rm C$错误；

$\rm D$．经分析知$A$最后静止于弹簧原长处，则当$A$、$B$都静止时$A$与$B$间的距离$\Delta x=x_{\text{B}}=\dfrac{4\mu mg}{k}$

选项$\rm D$正确。

故选：$\rm BD$。