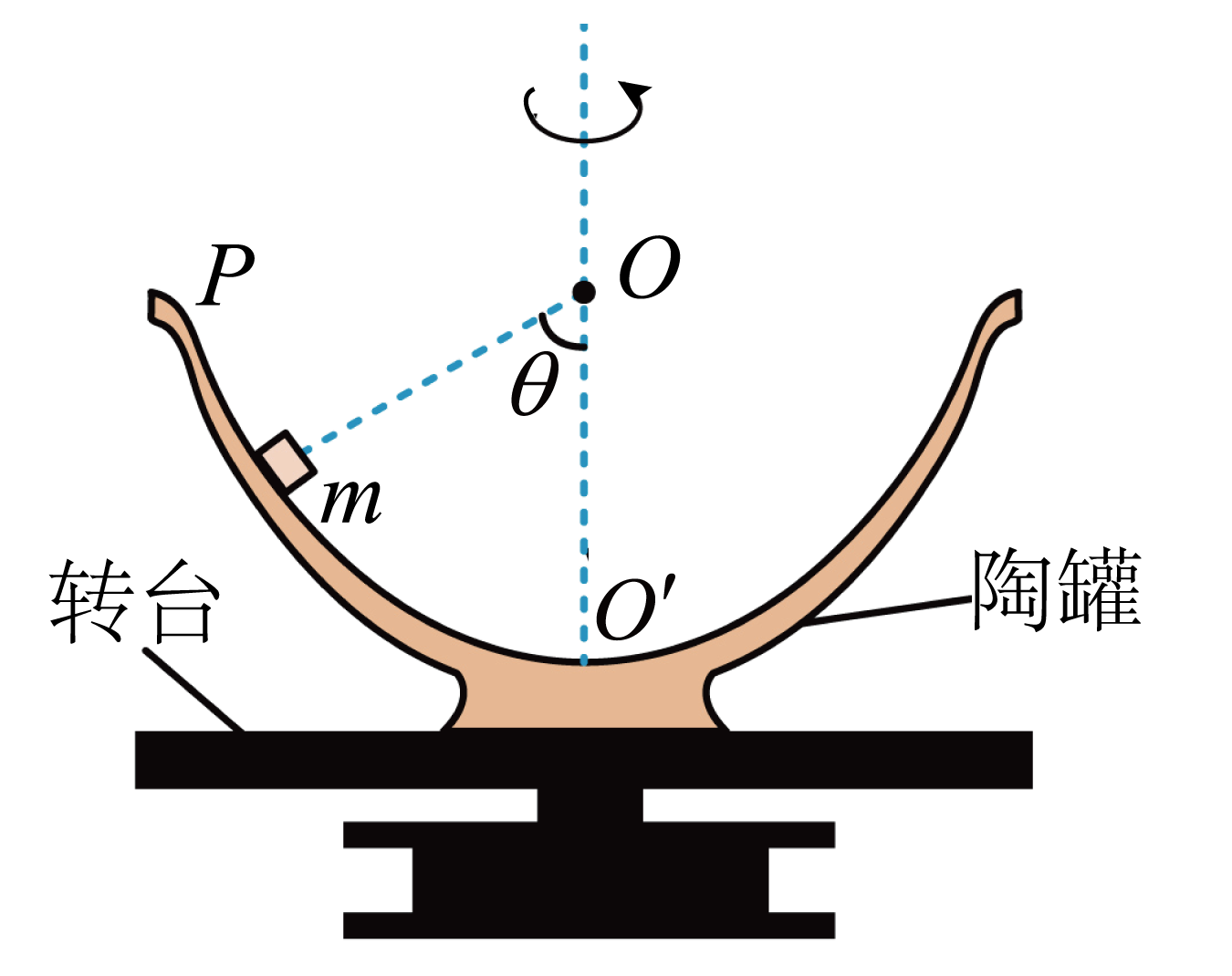
小物块的向心加速度；

$g\\tan \\theta$；

对小物块受力分析如图所示

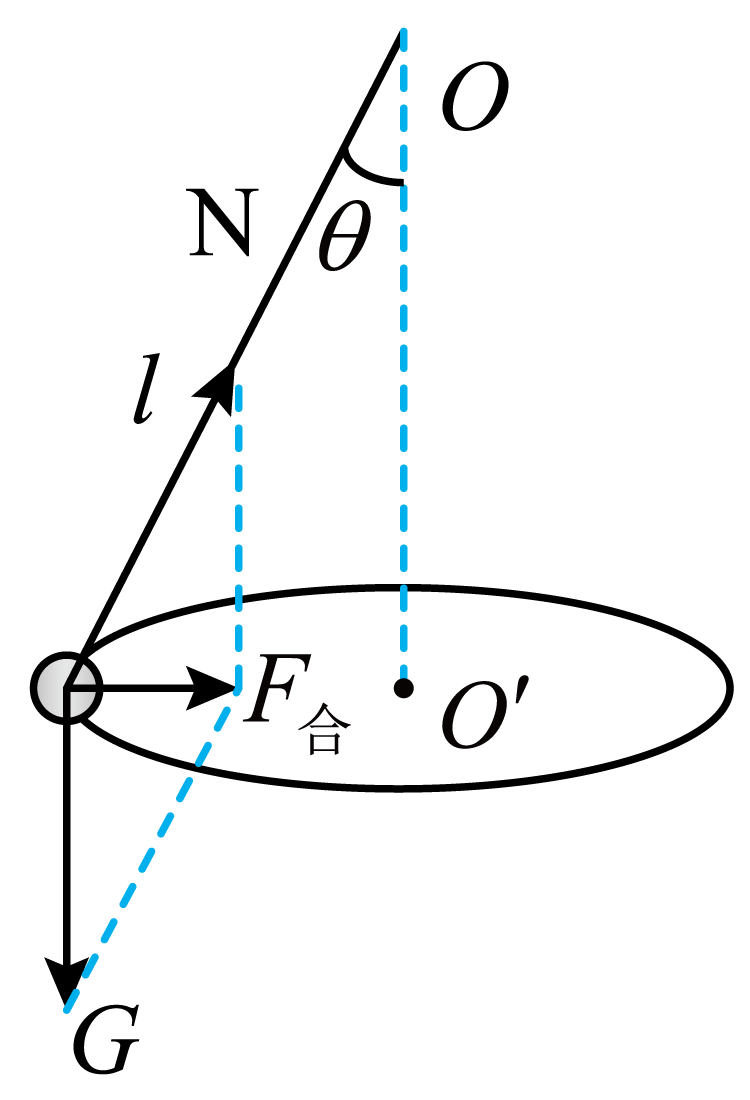
由牛顿第二定律得$mg\tan \theta=ma$

得小物块的向心加速度$a=g\tan \theta$

小物块的线速度；

$\\sqrt{gl\\sin\\theta\\tan\\theta}$；

由向心力公式得$mg\tan\theta=\dfrac{mv^{2}}{l\sin\theta}$

得$v=\sqrt{gl\sin\theta\tan\theta}$

小物块的周期。

$2\\pi\\sqrt{\\dfrac{l\\cos\\theta}{g}}$

由$T=\dfrac{2\pi r}{v}$

得$T=\dfrac{2\pi l\sin\theta}{\sqrt{gl\sin\theta\tan\theta}}=2\pi\sqrt{\dfrac{l\cos\theta}{g}}$