关于三个实验方案，下列说法正确的是$(\quad\ \ \ \ )$

甲、乙方案实验前均需要平衡摩擦力

甲、乙、丙方案均需要满足小车或滑块的质量远大于槽码的质量

乙方案中，小车加速运动时受到细线的拉力等于槽码所受重力的一半

A．由图示实验装置可知，甲、乙方案实验前均需要平衡摩擦力，故A正确；

B．由图示实验装置可知，甲实验中小车受到的拉力可以由力传感器测出，乙实验中小车所受拉力可以由弹簧测力计测出，甲、乙实验不需要方案不需要满足小车或滑块的质量远大于槽码的质量，故B错误；

C．由图示可知，乙方案中，小车加速运动时槽码向下加速运动，槽码处于失重状态，小车加速运动时受到细线的拉力小于槽码所受重力的一半，故C错误。

故选A。

某次甲方案实验得到一条纸带，部分计数点如图丁所示（每相邻两个计数点间还有$4$个计时点未画出），测得$s_{1}=3.71\ \text{cm}$，$s_{2}=7.92\ \text{cm}$，$s_{3}=12.63\ \text{cm}$，$s_{4}=17.86\ \text{cm}$。已知打点计时器所接交流电源频率为$\rm 50\ Hz$，则小车的加速度$a=$                    $\text{m/}{{\text{s}}^{\text{2}}}$（结果保留两位有效数字）。

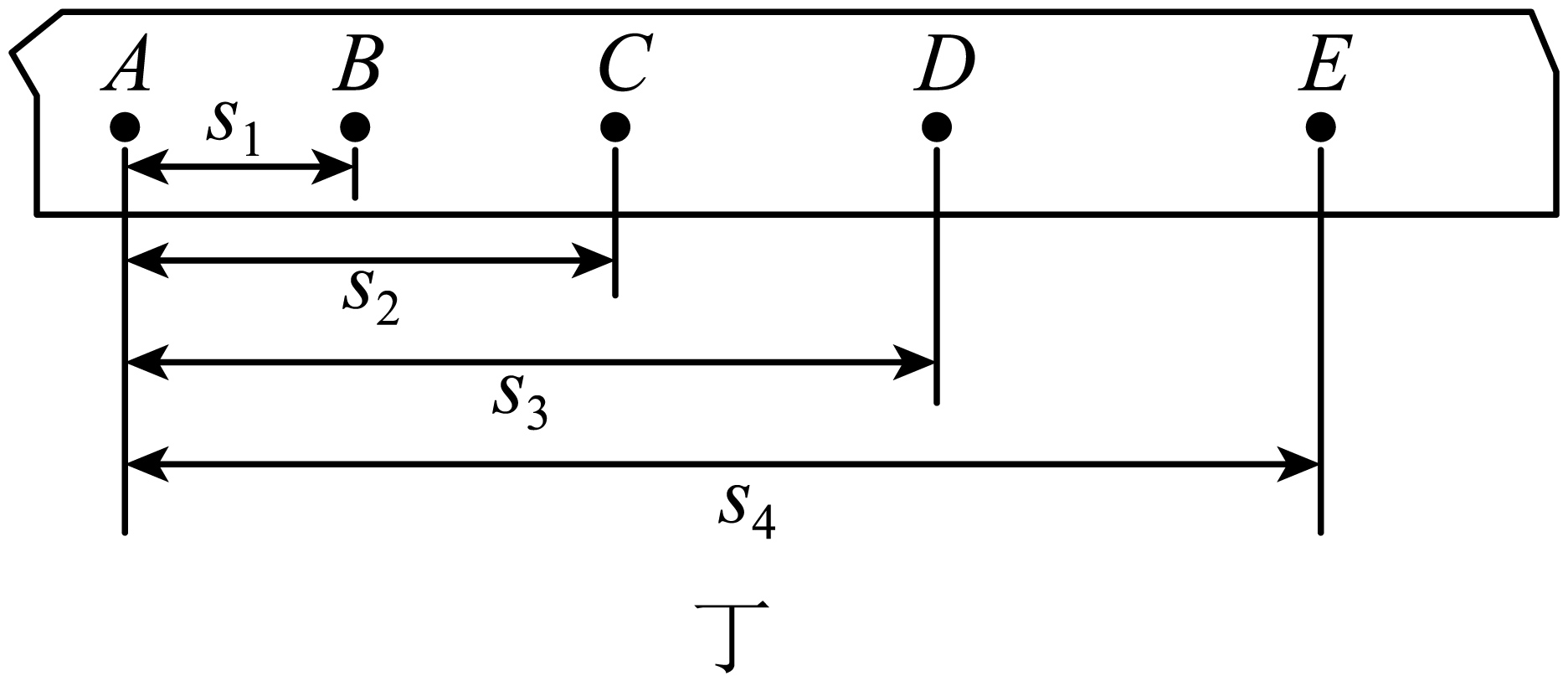
每相邻两个计数点间还有$4$个计时点未画出，打点计时器所接交流电源频率为$\rm 50\ Hz$，相邻计数点间的时间间隔$t=5T=\dfrac{5}{f}=\dfrac{5}{50}\ \text{s}=0.1\ \text{s}$

根据匀变速直线运动的推论$\Delta x=a{{t}^{2}}$由逐差法可知，小车的加速度大小$a=\dfrac{CD-AB+DE-BC}{4t^{2}}=\dfrac{CE-AC}{4t^{2}}=\dfrac{s_{4}-2s_{2}}{4t^{2}}=\dfrac{17.86-2\times7.92\times10^{-2}}{4\times0.1^{2}}\ \text{m}/\text{s}^{2}\approx0.51\ \text{m}/\text{s}^{2}$

甲方案实验中，以小车的加速度$a$为纵坐标、钩码的重力$F$为横坐标作出的$a-F$图像戊理想状态下应是一条过原点的直线，但由于实验误差影响，常出现如图所示的三种情况。关于这三种情况下列说法中正确的是$(\quad\ \ \ \ )$

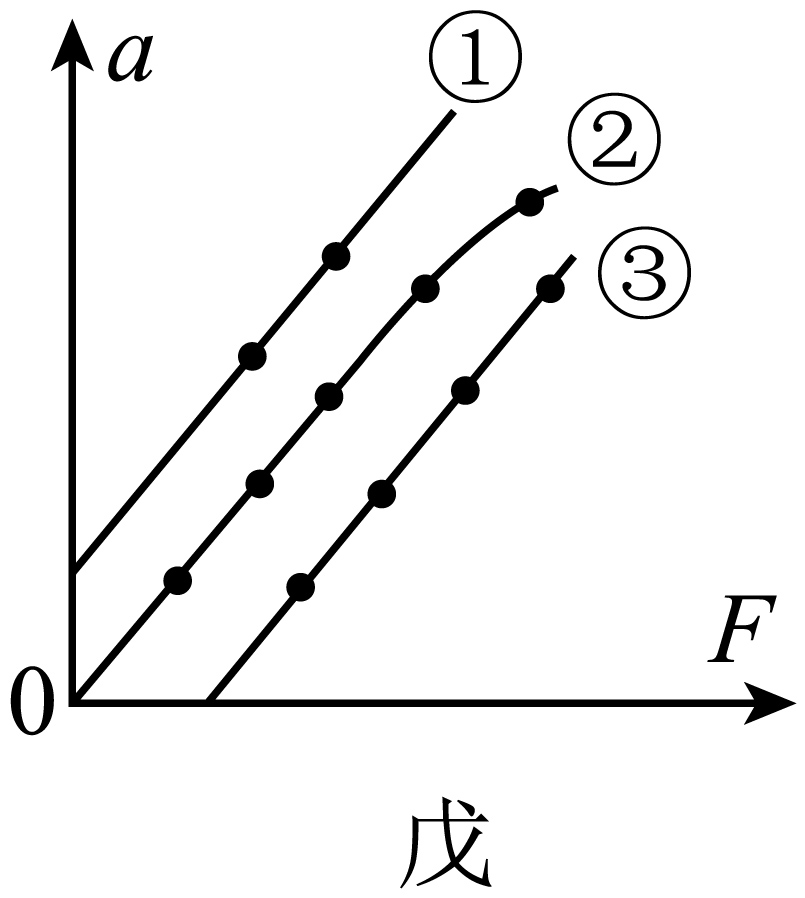
图线①交于纵轴的原因是钩码挂的个数太多

图线②右端弯曲的原因是钩码挂的个数太少

图线③交于横轴的原因可能是未平衡小车受到的阻力

$\rm A$．由图示图像可知，纵轴的截距大于$0$， $F$$=0$（即不挂钩码）时小车就具有了加速度；产生原因是平衡摩擦力时长木板的倾角过大，故$\rm A$错误；

$\rm B$．图线②在力较小时图像是直线，加速度与拉力成正比；拉力较大时图像向下弯曲，加速度偏小，由牛顿第二定律可得$F=Ma$，$mg-F=Ma$，解得$F=\dfrac{mg}{1+\dfrac{m}{M}}$，可知当$m\ll M$时，$F\approx mg$，$a-F$图像为直线，当钩码挂的个数太多时，不满足$m\ll M$，则$F\lt mg$，图像右端向下弯曲，所以图线②右端弯曲的原因是钩码挂的个数太多造成的，故$\rm B$错误；

$\rm C$．图线③在横轴的截距大于$0$，只有当$F$增加到一定值时，小车才获得加速度，产生原因是平衡摩擦力时长木板的倾角过小或未平衡小车受到的阻力，故$\rm C$正确。

故选$\rm C$。