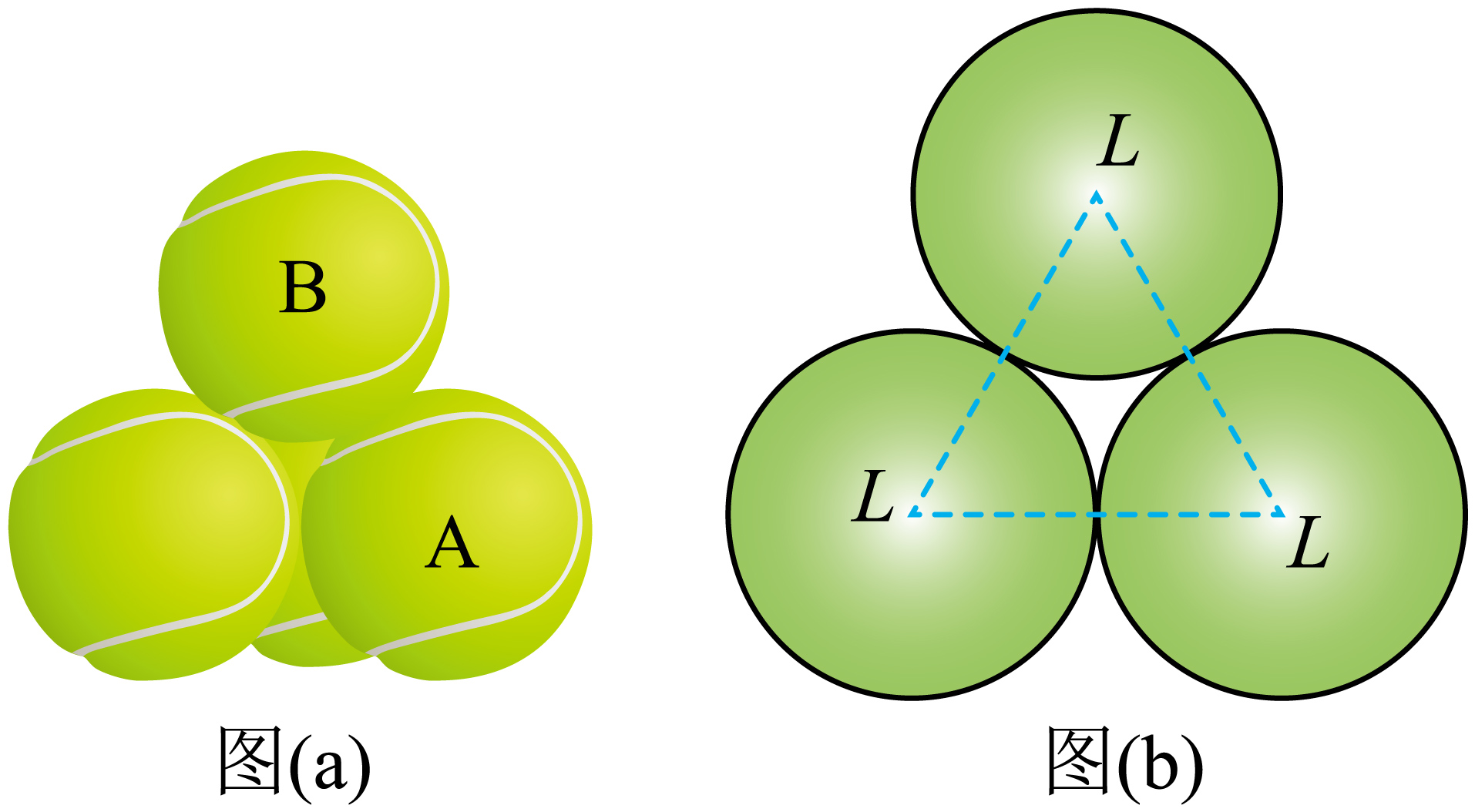
①如图（$a$）$4$个相同的网球紧挨叠放，静止在水平地面，若网球的质量为$m$，重力加速度为$g$，地面对网球$A$的支持力大小为                 ；

②图（$b$）是下层$3$球的俯视图，若稍微增大球心距离$L$，三球仍能静止，则网球$B$受到网球$A$的弹力大小                 

$\rm A$．增大      $\rm B$．减小      $\rm C$．不变

设地面对下面每个网球的支持力都为$F_{N}$，对四个网球整体受力分析可得$3F_{N}=4mg$

故地面对网球$A$的支持力为$F_{{N}}=\dfrac{4}{3}mg$

设下面三个球对$B$球的弹力为$F$，$AB$球心的连线与竖直方向的夹角为$\theta$，对$B$球受力分析有$mg=3F\cos \theta$

可知$A$球给$B$球的弹力大小为$F=\dfrac{mg}{3\cos\theta}$

当若稍微增大球心距离$L$时，$\theta$变大，故$A$球给$B$球的弹力增大；

故选：$\rm A$；

某同学使用网球训练器单人打回弹，如图，一轻质弹性绳将网球拴在底座中心$O$点，以$O$为原点在竖直平面内建直角坐标系$xoy$，将质量$m=60g$的网球从$A$点静止释放，落地后竖直弹起到最高点$B$，此时使用网球拍击打网球，网球瞬间获得水平速度$v=15\:\rm m/s$，网球运动到$C$点时，弹性绳恰好绷直，最后运动到$D$点与地面相撞。假设网球始终在竖直平面内运动，底座保持不动，忽略底座的高度、对球的大小、空气阻力以及对球旋转带来的影响，$g$取$10\:\rm m/s^{2}$。

①若网球第一次落地与地面接触的时间为$t=50\:\rm m/s$，撞击过程中损失的机械能为                 $\;\rm J$，地面对网球的平均作用力大小为                 $\;\rm N$。

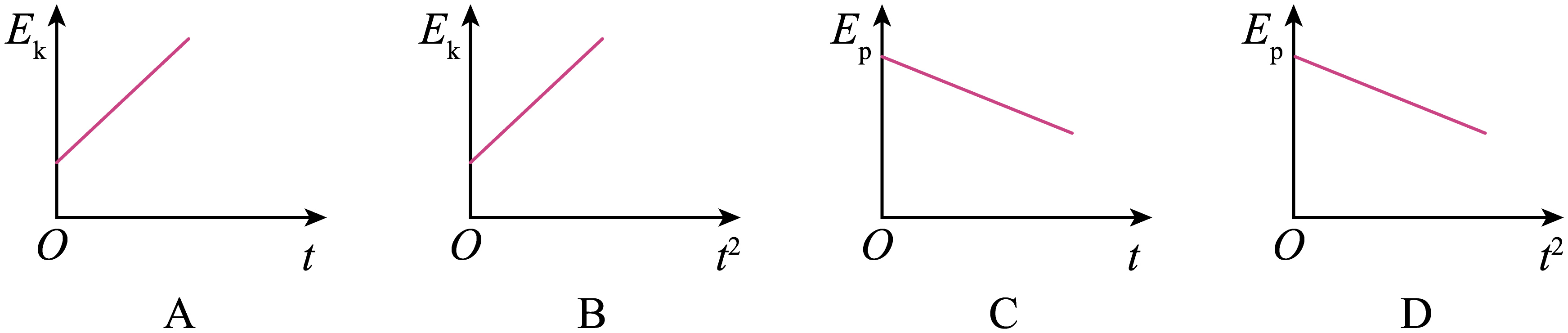
②网球从$B$运动到$C$过程中，动能$E_\rm {k}$和重力势能$E_\rm {p}$随时间$t$变化正确的是$(\qquad)$

③网球从$B$点运动到$C$点经历的时间为                 $\;\rm s$，网球在$C$点时重力的瞬时功率为                 $\;\rm W$。

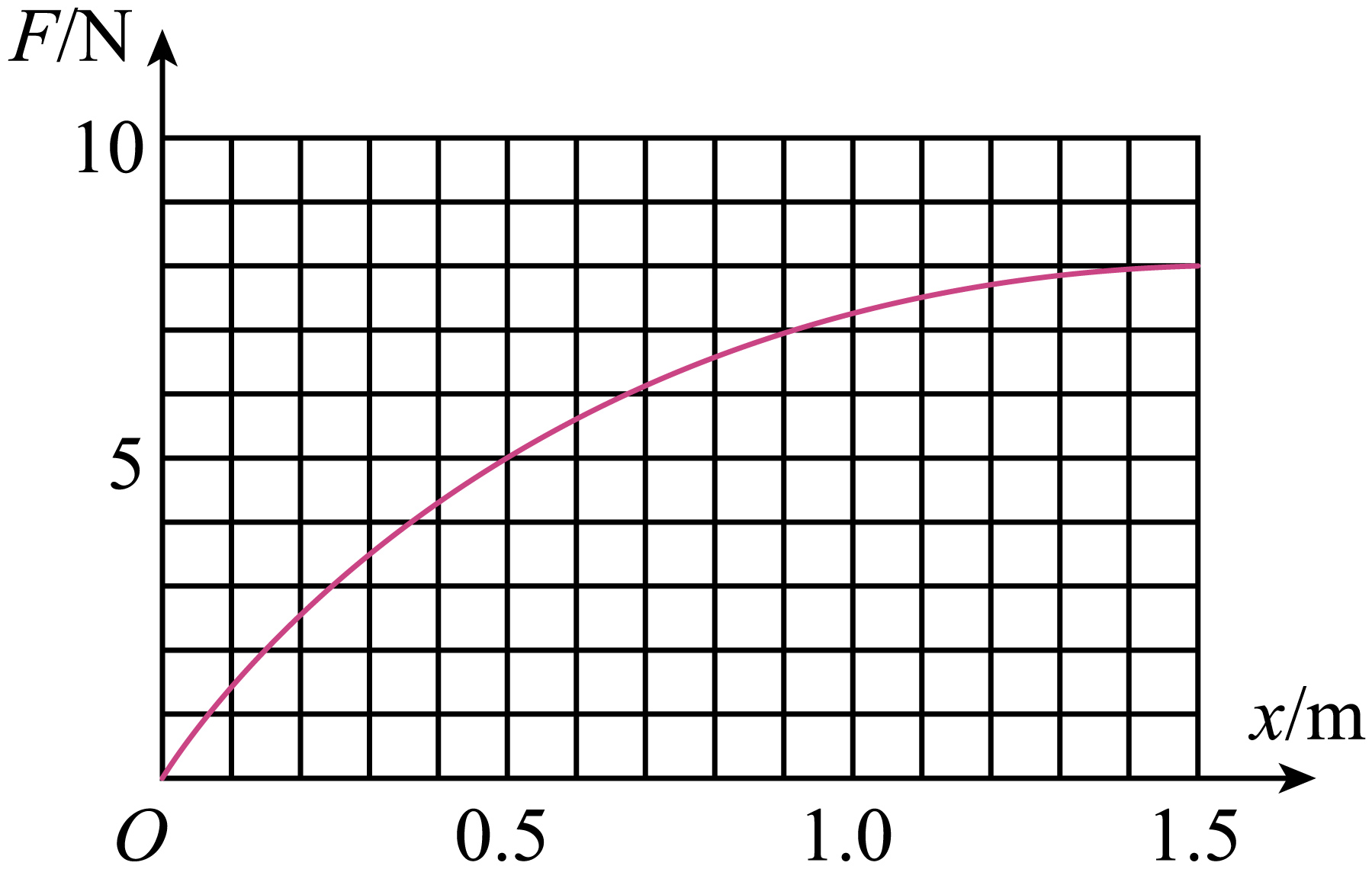
④如图所示为弹性绳所受拉力$F$与伸长量$x$之间的关系，当网球撞向$D$点时，弹性绳伸长量$x=1.0m$，此时弹性绳中的弹性势能为                 $\;\rm J$，网球的动能为                 $\;\rm J$。

网球从$A$点静止释放，做自由落体运动，由运动学公式可知落地速度为$v_{1}=\sqrt{2gh_{1} =}2\sqrt{10}\;\rm{m/s}$

网球落地后向上做竖直上抛运动，由运动学知识可知弹起后速度为$v_{2}=2\sqrt{5}\;\rm {m/s}$

故网球与地面撞击过程中损失的机械能为$\Delta E=\dfrac{1}{2}mv_{1}^{2}-\dfrac{1}{2}mv_{2}^{2}=0.6\;\rm{J}$

网球与地面作用过程中，以向下为正方向，由动量定理有$(mg-\overline{F})t=- mv_{2}-mv_{1}$

代入数据解得地面对网球的平均作用力大小为$\overline{F} \approx 13.6\;\rm{N}$

网球从$B$运动到$C$过程中由动能定理有$mgh=E_{\rm k} − E_{k0}$

网球从$B$运动到$C$过程中做平抛运动，由运动学知识有$h=\dfrac{1}{2}gt^{2}$

联立解得$E_{\rm{k}}=\dfrac{mg}{2}t^{2}+E_{{k0}}$

$\rm A$错误，$\rm B$正确；

网球从$B$运动到$C$过程中，由功能关系有$mgh=E_{p0} − E_{\rm p}$

联立解得$E_{\rm{p}}=E_{{p0}}-\dfrac{mg^{2}t^{2}}{2}$

$\rm C$错误，$\rm D$正确；

故选：$\rm BD$。

网球从$B$运动到$C$过程中做平抛运动，由运动学知识有$x=vt_{BC}$，$v_{Cy}=gt_{BC}$

可得网球从$B$点运动到$C$点经历的时间为$t_{BC}=0.2\;\rm s$

网球在$C$点时重力的瞬时功率为$P_{G}=mgv_{Cy}=1.2\;\rm W$

$F − x$图像的面积表示弹性绳上的弹力做功的多少，由图像可知，弹力做功为$W=-46 \times 1 \times 0.1\;\rm J=-4.6\;\rm J$

由功能关系可知此时弹性绳的弹性势能为$W=0 − E_\rm{p}$

即弹性绳的弹性势能为$4.6\;\rm J$

网球与弹性绳所组成的系统机械能守恒，由机械能守恒定律有$mgh_{BD}=E_{\rm p}+E_{kD} − E_{kB}$

联立解得当网球撞向$D$点时，网球的动能为$E_{kD}=2.75\;\rm J$。