质子质量为$m$、带电量为$q$，在直线加速器中由静止预加速后获得的动能为$E_{0}$，

①质子预加速后获得的速度大小$v_{0}=$                 。

②预加速过程，质子的电势能                 。

$\rm A$．增加$E_{0}$              $\rm B$．增加$2E_{0}$              $\rm C$．减少$E_{0}$              $\rm D$．减少$2E_{0}$

③若直线加速器内匀强电场的电场强度为$E$，则质子加速的距离$L=$                 。

根据动能的表达式是$E_{0}=\dfrac{1}{2}mv_{0}^{2}$

解得$v_{0}=\sqrt{\dfrac{2E_{0}}{m}}$

根据动能定理可知，预加速过程电场力对质子做的功$W=E_{0}$

故质子的电势能减少了$E_{0}$

故选：$\rm C$

设匀强电场的电场强度为$E$，根据动能定理$EqL=E_{0}$

解得$L=\dfrac{E_{0}}{Eq}$

质子在同步加速器加速的简化模型如图所示。带电量为$q$的质子以初动能$E_{0}$进入两块平行金属板，金属板中间开有小孔。质子每次进入两板间时，两板间的电势差变为$U$，粒子得到加速；当质子离开金属板时，两板上的电荷量均立即变为零。两板外部存在垂直于纸面向里的匀强磁场，质子在磁场作用下做半径为$R$的圆周运动，$R$远大于板间距离。质子经电场多次加速，动能不断增大，为使$R$保持不变，磁场必须相应地变化。不计粒子加速时间及其做圆周运动产生的电磁辐射，不考虑磁场变化对粒子速度的影响及相对论效应。求：

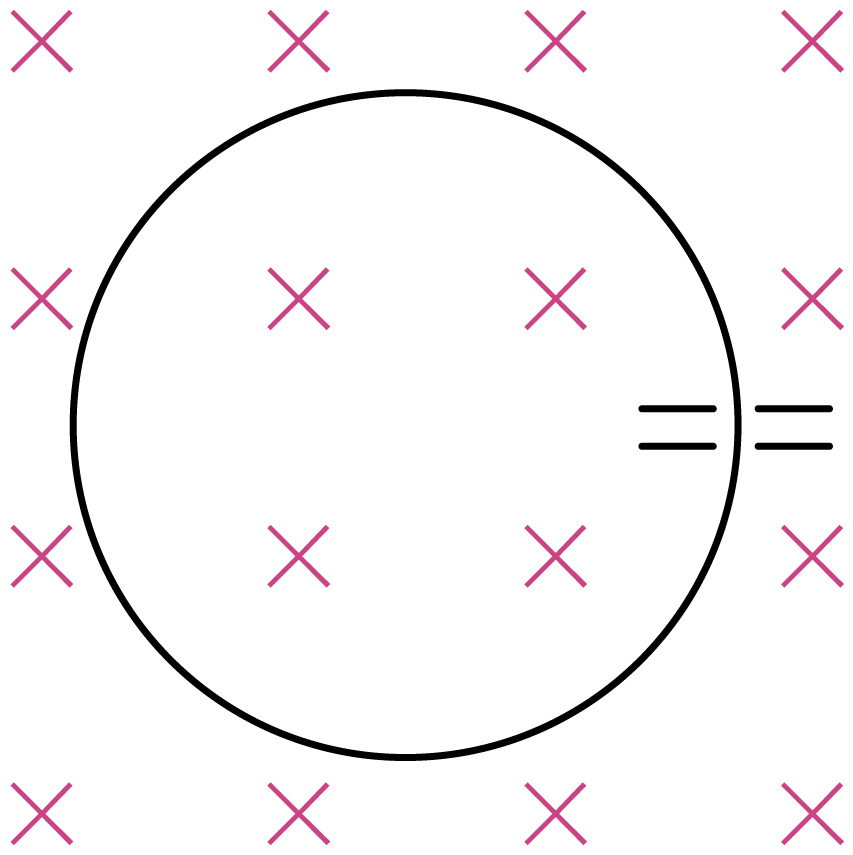
①质子第一次离开金属板时的速度大小$v_{1}$；

②质子在第一周运动（加速一次）时磁场的磁感应强度的大小$B_{1}$；

质子在运动的第$n$周内电场力对粒子做功的平均功率$\overline{P}$。

① $\\sqrt{\\dfrac{2\\left( Uq+E_{0} \\right)}{m}}$ ；②$\\dfrac{1}{qR}\\sqrt{2m\\left( U_{q}+E_{0} \\right)}$； ③$\\dfrac{Uq}{\\pi R}\\sqrt{\\dfrac{nUq+E_{0}}{2m}}$

根据动能定理$Uq=\dfrac{1}{2}mv_{1}^{2}-E_{0}$

解得$v_{1}=\sqrt{\dfrac{2\left( Uq+E_{0} \right)}{m}}$

带电粒子在磁场中运动$qv_{1}B_{1}=m\dfrac{v_{1}}{R}$

解得$B_{1}=\dfrac{1}{qR}\sqrt{2m\left( U_{q}+E_{0} \right)}$

设质子经$n$次加速后的速度为$v_{2}$，根据动能定理$nUq=\dfrac{1}{2}mv_{2}^{2}-E_{0}$

解得$v_{2}=\sqrt{\dfrac{2nUq+2E_{0}}{m}}$

此时质子在磁场中做圆周运动的周期为$T=\dfrac{2\pi R}{v_{2}}$

所以质子在运动的第$n$周内电场力对粒子做功的平均功率$\overline{P}=\dfrac{Uq}{T}=\dfrac{Uq}{\pi R}\sqrt{\dfrac{nUq+E_{0}}{2m}}$