若导体棒在直轨道$ac(bd)$上的动摩擦因数$\mu =0.5$，圆弧轨道$ce(df)$的半径$r=2\:\rm m$，角度$\theta=37^\circ$，释放高度$H=3\:\rm m$，导体棒质量$m=1\:\rm kg$。则：

①导体棒在直轨道$ac(bd)$上运动的加速度大小$a=$                 $\;\rm m/s^{2}$，$1\;\rm s$末重力的瞬时功率$P_{1}=$                 $\;\rm W$；

根据牛顿第二定律得导体棒在直轨道$ac(bd)$上运动的加速度大小$a=g\sin\theta-\mu g\cos\theta=2\;\rm m/s^{2}$

$1\;\rm s$末的速度为$v=at=2\;\rm m/s$

$1\;\rm s$末重力的瞬时功率$P_{1}=mgv\sin \theta=12\;\rm W$；

导体棒到达圆弧轨道的底端$ef$处对轨道的压力大小；

$24\\;\\rm N$

导体棒从释放到圆弧轨道的底端$ef$处，由动能定理得$mg\left( H+r-r\sin\theta \right)-\mu mg\cos\theta \times \dfrac{H}{\sin\theta}=\dfrac{1}{2}mv_{1}^{2}$

导体棒到达圆弧轨道的底端$ef$处，由牛顿第二定律得$F_{{N}}-mg=\dfrac{mv_{1}^{2}}{r}$

解得$F_{N}=24\;\rm N$

由牛顿第三定律得导体棒到达圆弧轨道的底端$ef$处对轨道的压力大小为$24\;\rm N$；

已知定值电阻为$R$，导体棒电阻为$R_{0}$，水平导轨间距为$l$，磁场的磁感应强度大小为$B$。导体棒以速度$v_{0}$进入正方形阴影区域磁场后，受到一个水平向右的外力$F$作用。

①在图（$c$）中标出通过导体棒的感应电流方向                。

②若导体棒在磁场中做匀速直线运动，则外力$F$的表达式为                。

③若导体棒质量为$m$，进入磁场后做加速度为$a$的匀加速直线运动。

$i.$（简答）求外力$F$与瞬时速度$v$的函数关系式                。（结果用字母表示）

$ii.$导体棒与磁场左边界的距离为$x$，若导体棒在出磁场前就撤去外力，定性画出导体棒在磁场中运动可能出现的“$v-x$”图线                。（作图题，不需要写出演算过程）

见解析 $\\dfrac{B^{2}L^{2}v_{0}}{R+R_{0}}$ $ma$$+$$\\dfrac{B^{2}L^{2}v}{R+R_{0}}$ 见解析

由右手定则知导体棒中的电流方向如图所示

导体棒切割磁感线产生的感应电动势和电流分别为

$E=BLv_{0}$，$I=\dfrac{E}{R+R_{0}}$

导体棒受到的安培力$F_{安}=BIL=\dfrac{B^{2}L^{2}v_{0}}{R+R_{0}}$

若导体棒在磁场中做匀速直线运动，外力等于安培力$F=F_{安}=\dfrac{B^{2}L^{2}v_{0}}{R+R_{0}}$

当导体棒的速度为$v$时，由牛顿第二定律得$F'-{F_{安}}'=F-\dfrac{B^{2}L^{2}v}{R+R_{0}}=ma$

解得$F'=\dfrac{B^{2}L^{2}v}{R+R_{0}}+ma$

撤去外力前，导体棒在磁场中做匀加速运动，有$v^{2} − v_{0}^{2}=2ax$

整理得$v=\sqrt{v_{0}^{2}+2ax}$

由数学知识知图像为

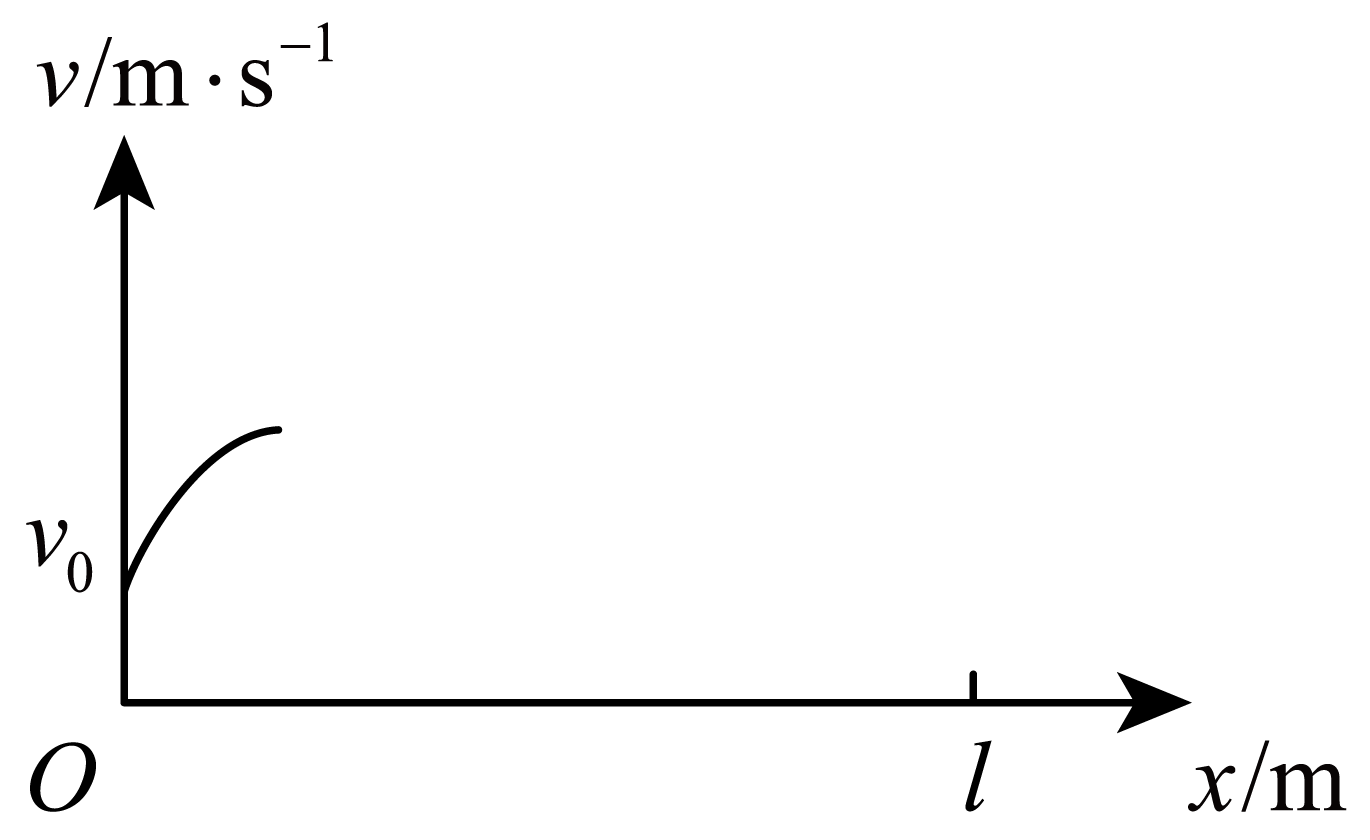
设撤力瞬间导体棒的速度为$v_{1}$，撤去力$F$后，由动量定理得$- \sum\dfrac{B^{2}L^{2}v}{R+R_{0}} \cdot \Delta t=mv'-mv_{1}$

整理得$v'=v_{1}-\dfrac{B^{2}L^{2}x}{R+R_{0}}$

图像为斜向下的直线，由于磁场宽度未知，无法判断何时减速至$0$，故可能的图像为