如图（$a$）所示，一个总电阻为$R$的单匝正方形线圈在一个变化的磁场中，穿过线圈的磁通量随时间的变化如图（$b$）所示。则在半周期内通过线圈的电荷量为                 ；一个周期内流过线圈的电流有效值为                 ；（以上两空结果均用“$\Phi_{0}$、$R$、$T$”表示）

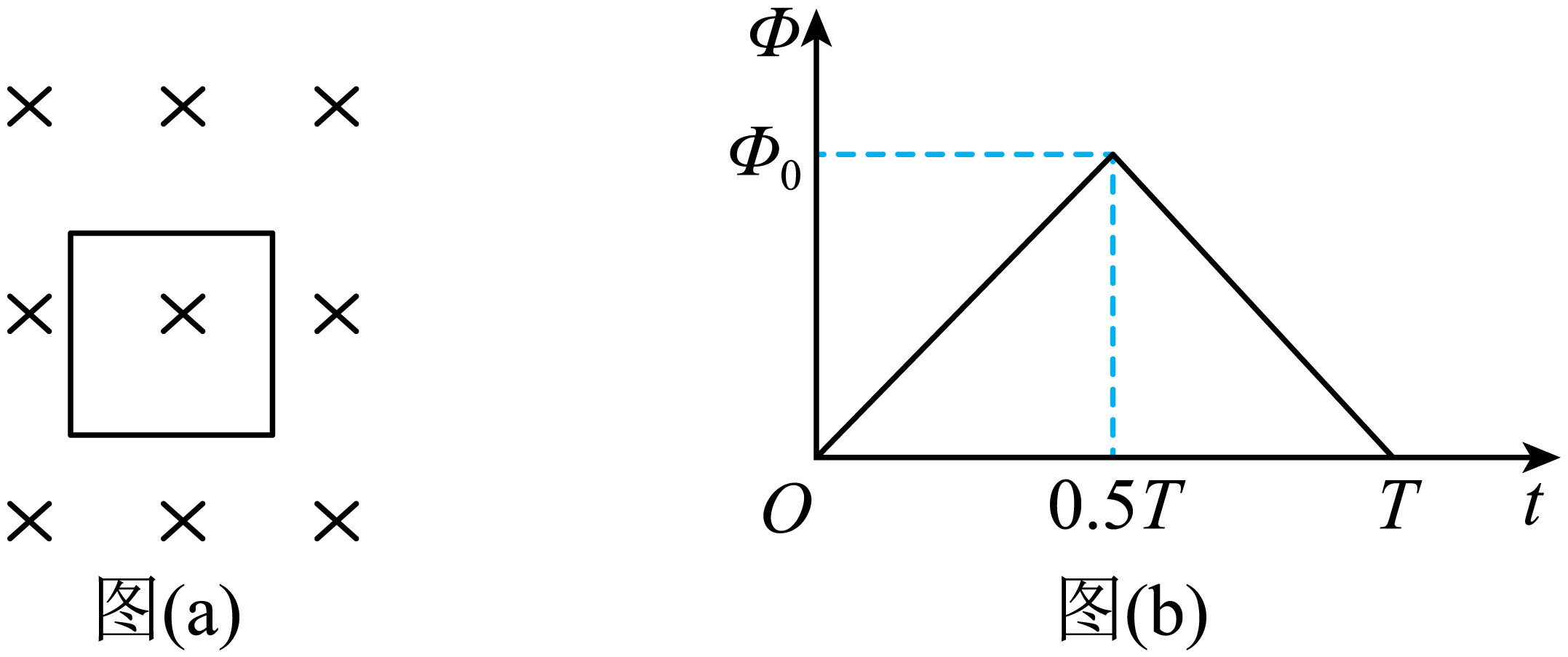
由题意，在半周期内通过线圈的电荷量为$q=It=\dfrac{E}{R}t=\dfrac{\Delta\Phi}{R}= \dfrac{\Phi_{0}}{R}$

根据图（$b$），可得一个周期内流过线圈的电流有效值为$I=\dfrac{E}{R}=\dfrac{\Delta\Phi}{\Delta tR}=\dfrac{\Phi_{0}-0}{0.5T \times R}=\dfrac{2\Phi_{0}}{TR}$；

如图所示，线圈在磁场中转动且切割磁感线可以在端口$A$、$B$处输出交变电压。线圈顺时针转动，从线圈平面处于中性面时开始计时，在第一个周期$T$内，转动的角速度恒定。

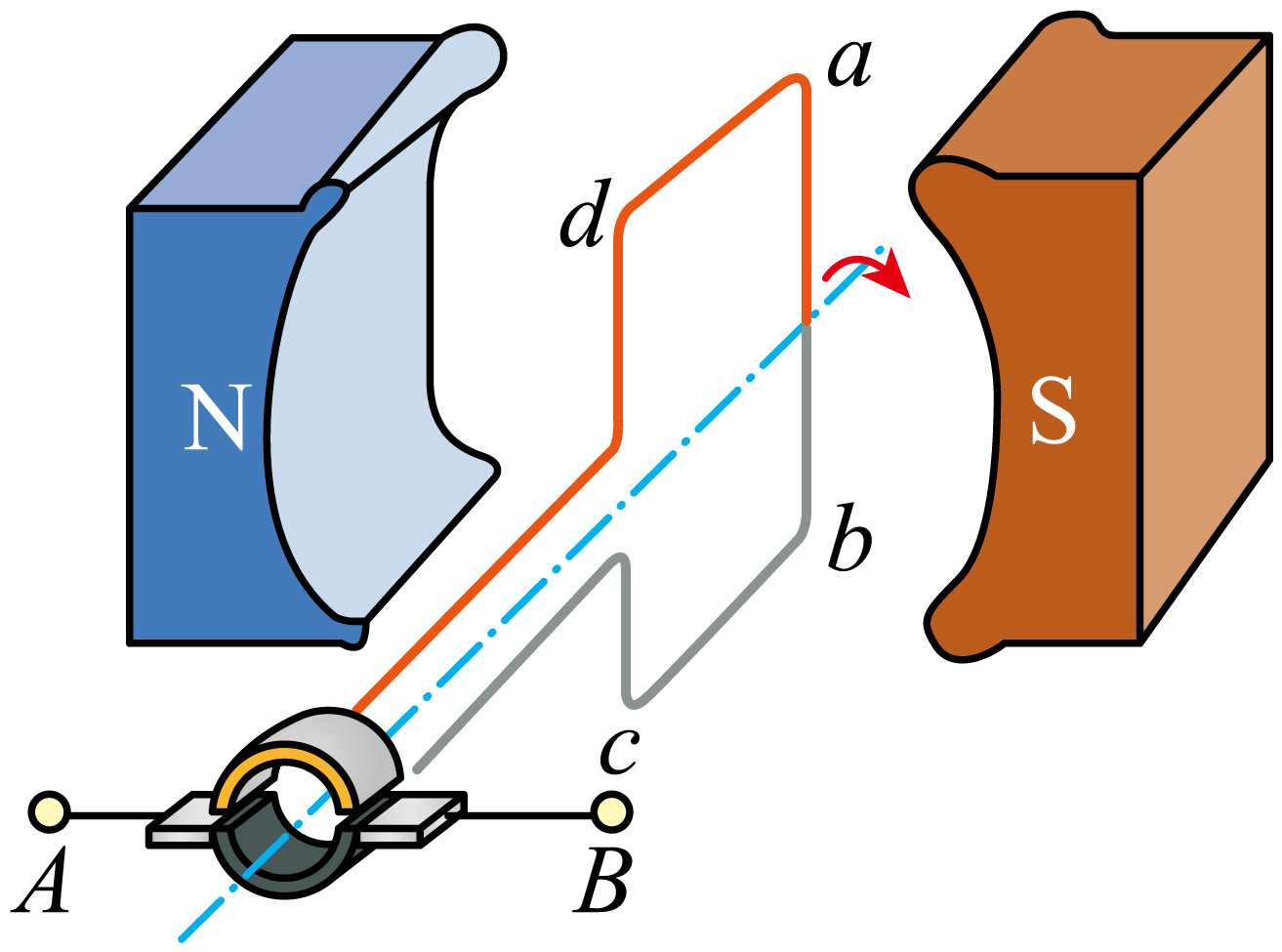
①当$t=0.25T$时，$ad$边上感应电流的方向为               。

$\rm A$．$a$到$d$                  $\rm B$．$d$到$a$

②如图所示，在$A$、$B$两端接一个阻值为$R$的电阻，线圈在第一个周期内克服安培力做功为$W$。线圈内阻为$0.5R$，则电阻上产生的热量为               。

$\rm A$．$W$                      $\rm B$．$\dfrac{1}{3}W$

$\rm C$．$\dfrac{2}{3}W$                   $\rm D$．$\dfrac{3}{2}W$

③如图所示，在$A$、$B$端口处接一个家用低压变压器，在实际使用过程中发现其微微发热。当$U_{AB}=6.0\;\rm V$时，表中“$★$”的数据最符合实际的是               

$\rm A$．$12.0\;\rm V$      $\rm B$．$11.3\;\rm V$      

$\rm C$．$3.0\;\rm V$      $\rm D$．$2.8\;\rm V$

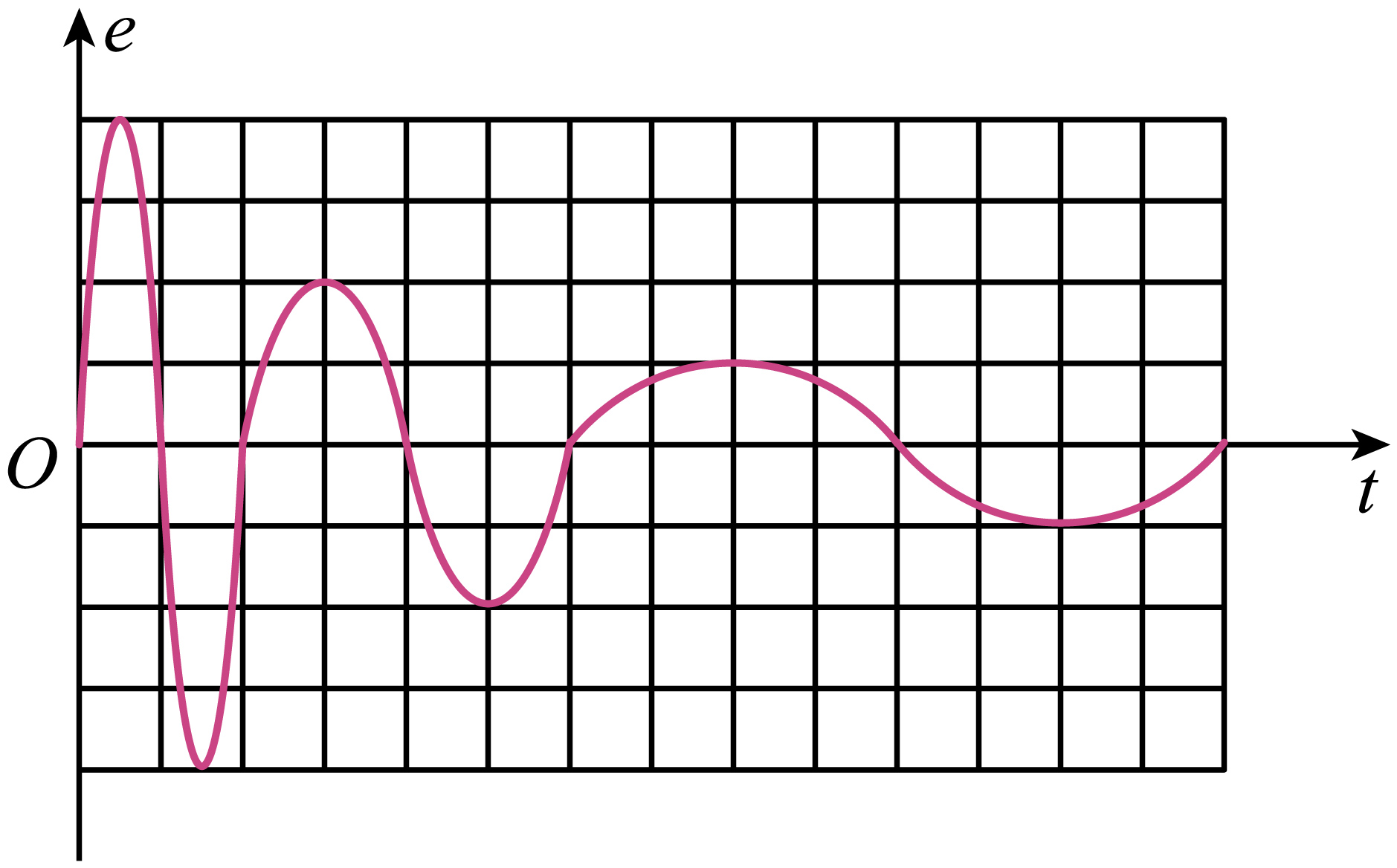
④若线圈产生的正弦交流电动势随时间变化的$e-t$图像按如图所示呈规律性变化，其中第一个周期内线圈产生的电能为$W_{0}$。经过足够长的时间$A$、$B$输出的总电能为$0.8W_{0}$。则整个过程中线圈的效率为                  。

$\rm A$．$80.0\%$              $\rm B$．$64.0\%$

$\rm C$．$40.0\%$              $\rm D$．$26.7\%$

①从线圈平面处于中性面时开始计时，根据右手定则，可判断知$t=0.25T$时，$ad$边上感应电流的方向为$a$到$d$ 。

故选：$\rm A$。

②线圈在第一个周期内克服安培力做功为$W$，根据功能关系可知$W=Q_{1}+Q_{2}$，$Q_{1}=I^{2} \times 0.5RT$，$Q_{2}=I^{2} \times RT$

则电阻上产生的热量为$Q_{2}=\dfrac{R}{0.5R+R}W=\dfrac{2}{3}W$

故选：$\rm C$。

③若该变压器为理想变压器，根据理想变压器电压与匝数比关系$\dfrac{U_{1}}{U_{2}}=\dfrac{n_{1}}{n_{2}}$

可得$U_{CD}=U_{AB} \times \dfrac{n_{2}}{n_{1}}=6 \times \dfrac{800}{400}\;\rm V=12\;\rm V$

但由于在实际使用过程中发现其微微发热，即输出端的功率小于输入端的功率，则输出端的电压$U_{CD}$真实值应比理论值稍小一些。

故选：$\rm B$。

④第一个周期内线圈产生的电能为$W_{0}$，经过足够长的时间$A$、$B$输出的总电能为$0.8W_{0}$。则整个过程中线圈的效率为$\eta=\dfrac{0.8W_{0}}{W_{0}} \times 100\%=80\%$。

故选：$\rm A$。