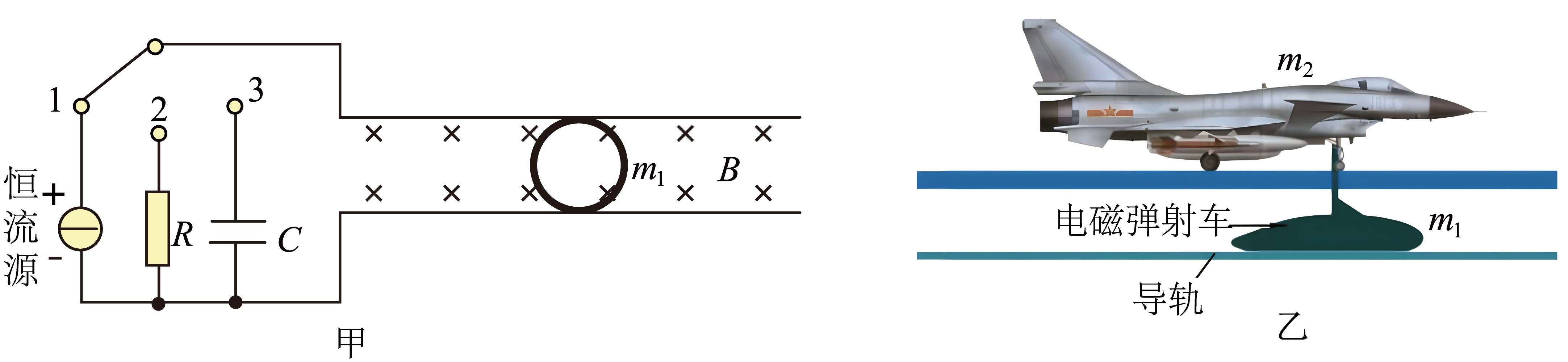
求圆环接入电路的电阻值$r$和模型飞机的加速时间$\Delta t$；

$2\\;\\rm s$；

金属环在导轨问两段圆弧并联接入电路中，每段圆环的电阻$R=\dfrac{R_{1}}{2}$

由串并联关系，侧环接入的总电阻为$r=\dfrac{R}{2}$

故$r=0.1\;\rm \Omega$

对金属环和飞机模型整体受力分析，在安培力的作用下做匀加速直线运动，受到安培力为$F=BIl$

由牛顿第二定律有$F=(m_{1}+m_{2})a$

由匀变速直线运动规律有$v_{1}=a ⋅ \Delta t$

代入数据得：$\Delta t=2\;\rm s$；

若飞机起飞瞬间将开关立即郑向$2$，与$R=0.1\;\rm \Omega$的电阻接通，求此后电阻$R$上产生的焦耳热；

$5.0\\;\\rm J$；

金属环的动能变成全电路的焦耳热为$Q= \dfrac{1}{2}m_{1}v_{1}^{2}$

环接入电路的电阻和$R$相同有$Q_{R}=\dfrac{R}{R_{1}+R}Q$

则有：$Q_{R}=\dfrac{1}{4}mv^{2}$

代入数据得$Q_{R}=5.0\;\rm J$；

若飞机起飞瞬间将开关立即掷向$3$，与$C=15\;\rm F$的电容器接通，求金属环稳定时的速度$v_{2}$。

$5\\;\\rm m/s$。

当圆环稳定运动时，设速度为$v_{2}$，此时电容器上带的电量为$Q=CBdv_{2}$

电容器的电量的变化即为道过环的电量为$\Delta Q=Q-0=\overline{I}t$

对圆环，由动量定理有$- B\overline{I}dt=mv_{2}-mv_{1}$

由以上公式有：$v_{2}=\dfrac{mv_{1}}{m+CB^{2}d^{2}}$

代入数据得$v_{2}=5\;\rm m/s$。