示波器是一种多功能电学仪器，它是由加速电场和偏转电场组成的。如图所示，质量为$m$的带电粒子由静止开始经加速电场加速后，沿平行于板面的方向从正中间射入偏转电场，并从另一侧射出。已知带电粒子的电荷量为$q$，加速电场电压为$U_{1}$，偏转电场的极板长度为$L$，两极板间的距离为$d$，偏转电场极板间的电压为$U_{2}$且可调节，不计粒子的重力。则下列说法正确的是$(\qquad)$

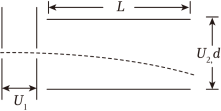
粒子离开偏转电场时的动能为$q(U_{1}+U_{2})$

同种电性的不同带电粒子，射出装置的位置相同

减小$U_{2}$，带电粒子通过偏转电场的时间变长

若粒子刚好从下极板边缘离开偏转电场，则$\\dfrac{U_2}{U_1}=\\dfrac{2{d^2}}{L^2}$

$\rm A$、对粒子从静止到离开偏转电场，由动能定理得：$E_{k}-0=W_{1}+W_{2}$

可知粒子离开偏转电场获得的动能等于加速电场做功$W_{1}$和偏转电场做功$W_{2}$，其中$W_{1}=qU_{1}$，$W_{2}\ne qU_{2}$

所以粒子离开偏转电场时的动能并不等于$q(U_{1}+U_{2})$，故$\rm A$错误；

$\rm B$、带电粒子在加速电场中，由动能定理有$q{U_1}=\dfrac{1}{2}mv_1^2$，可得${v_1}=\sqrt{\dfrac{2q{U_1}}{m}}$

带电粒子在偏转电场中做类平抛运动，水平方向做匀速直线运动，由于粒子从另一侧射出，则在偏转电场极板间运动的时间为$t=\dfrac{L}{v_1}=L\sqrt{\dfrac{m}{2q{U_1}}}$

带电粒子在偏转电场极板间的加速度为$a=\dfrac{F}{m}=\dfrac{{U_2}q}{md}$

竖直方向的位移为$y=\dfrac{1}{2}a{t^2}=\dfrac{{U_2}{L^2}}{4{U_1}d}$

根据上式可知，带电粒子在电场中偏转，不同带电粒子均从同一位置射出，偏移量与比荷无关，只与装置本身有关，所以同种电性的不同带电粒子，射出装置的位置相同，故$\rm B$正确；

$\rm C$、减小偏转电压并不会影响离开偏转电场的时间，因为该时间由水平位移和水平速度决定，因此时间不变，故$\rm C$错误；

$\rm D$、若刚好从下极板边缘射出，根据偏移量公式有：$\dfrac{d}{2}=\dfrac{{U_2}{L^2}}{4{U_1}d}$，解得：$\dfrac{U_2}{U_1}=\dfrac{2{d^2}}{L^2}$，故$\rm D$正确。

故选：$\rm BD$。