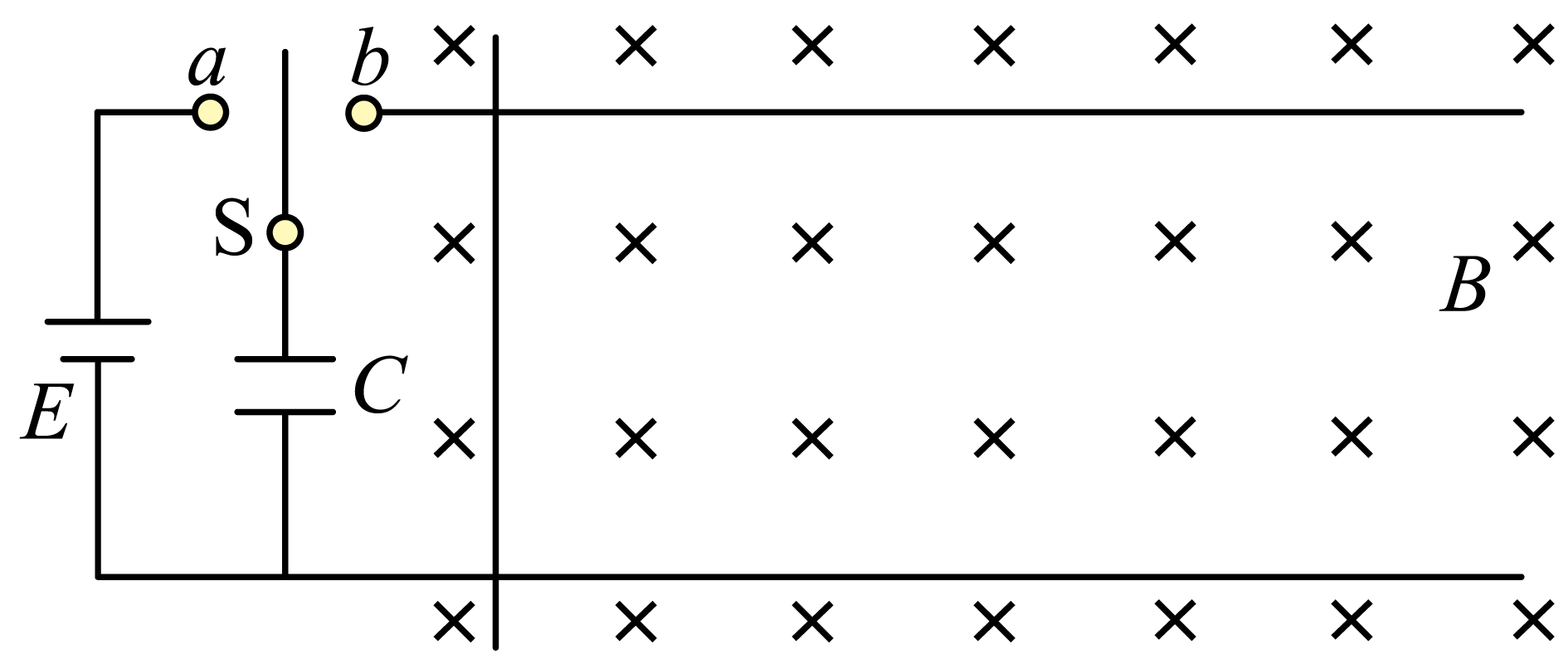
两根长直光滑平行金属导轨固定在绝缘水平桌面上，导轨间距为$L$，空间存在垂直于导轨平面向下、磁感应强度为$B$的匀强磁场，俯视角度如图所示。导轨左端通过单刀双掷开关与电源、电容器相连，电源电动势为$E$（内阻不计），电容器的电容为$C$。将质量为$m$，电阻为$R$的导体棒垂直放置在导轨上，先将开关接到$a$，待电容充电结束后将开关换接到$b$。忽略导线和导轨电阻，且不考虑电磁辐射及回路中电流产生的磁场，下列说法正确的是$(\qquad)$

导体棒加速度的最大值为$\\dfrac{BLE}{MR}$

导体棒能够达到的最大速度为$\\dfrac{E}{BL}$

导体棒从开始运动至达到最大速度的过程中，通过导体棒横截面积的电荷量为$\\dfrac{CmE}{{{B}^{2}}{{L}^{2}} C+m}$

导体棒达到最大速度时，电容器极板间的电压为$\\dfrac{BLE}{{{B}^{2}}{{L}^{2}} C+m}$

$\rm A$．充电后，电容器电压为$E$。开关接到“$a$”时导体棒速度为$0$，电容器两端电压的最大值为$E$，导体棒中电流最大为$I_{\rm m}$，导体棒所受安培力的最大值为$F_{\rm m}$，加速度最大设为$a_{\rm m}$，故${{I}_{\text{m}}}=\dfrac{E}{R}$，${{F}_{\text{m}}}={{I}_{\text{m}}}LB$，${{F}_{\text{m}}}=m{{a}_{\text{m}}}$

解得${{a}_{\text{m}}}=\dfrac{BEL}{mR}$，故$\rm A$正确；

$\rm BCD$．导体棒达到最大速度$v_{\rm m}$时，电路中电流为$0$，电容器两端电压为$U$，电容器放出的电荷量为$\Delta Q$，导体棒达到最大速度时，电容器两端电压等于金属杆切割磁感线产生的感应电动势$U=BL{{v}_{\text{m}}}$

故电容器放电量为$\Delta Q=C(E-U)$

由动量定理$\sum{I}LB\Delta t=m{{v}_{\text{m}}}$

又$\sum{I}\Delta t=\Delta Q$

解得${{v}_{\text{m}}}=\dfrac{CEBL}{{{B}^{2}}{{L}^{2}}C+m}$，$\Delta Q=\dfrac{CmE}{{{B}^{2}}{{L}^{2}} C+m}$，$U=\dfrac{CE{{B}^{2}}{{L}^{2}}}{{{B}^{2}}{{L}^{2}}C+m}$，故$\rm BD$错误，$\rm C$正确。

故选：$\rm AC$。