| 双棒模型 题目答案及解析
稿件来源:高途
| 双棒模型题目答案及解析如下,仅供参考!
选修3-2
第四章 电磁感应
4.4 法拉第电磁感应定律
双棒模型
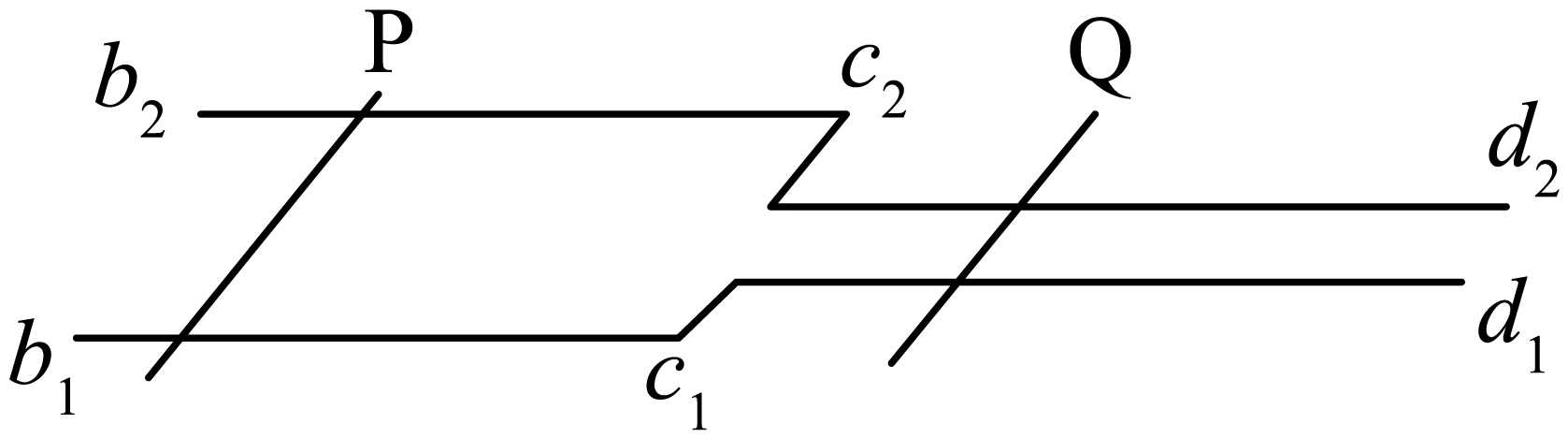
如图所示,足够长的光滑水平轨道左侧${{b}_{1}}{{b}_{2}}\sim {{c}_{1}}{{c}_{2}}$部分的轨道间距为$3L$,右侧${{c}_{1}}{{c}_{2}}\sim {{d}_{1}}{{d}_{2}}$部分的轨道间距为$L$,两部分轨道通过导线连通。整个区域存在竖直向下的匀强磁场(图中未画出),磁感应强度大小$B=0.1\;\rm \text{T}$。质量$m=0.1\;\rm {kg}$的金属棒和质量$\mathrm{M}=0.2 \;\rm {kg}$的金属棒$Q$垂直于导轨分别静止放置在左、右两侧轨道上。现给金属棒$P$一大小为${{v}_{0}}=2\;\rm \text{m}/\text{s}$、方向沿轨道向右的初速度,已知两金属棒接入电路的有效电阻均为$R=0.2\;\rm \Omega$,轨道电阻不计,$L=0.2\;\rm \text{m}$,两金属棒在运动过程中始终相互平行且与导轨保持良好接触,棒总在宽轨上运动,$Q$棒总在窄轨上运动。下列说法正确的是$(\qquad)$
整个过程金属棒$P$、$Q$动量守恒
","金属棒$P$匀速运动的速度大小为$\\dfrac{2}{19}{\\;\\rm m/s}$
","整个过程通过金属棒$Q$某横截面的电荷量为$\\dfrac{60}{19}{\\;\\rm C}$
","整个运动过程金属棒、$Q$扫过的面积之差为$\\dfrac{120}{19}{{\\;\\rm {m}}^{2}}$
"]$\rm A$.因为$P$、$Q$受到的安培力大小不相等,合力不为零,所以整个过程金属棒$P$、$Q$动量不守恒,$\rm A$错误;
$\rm B$.选取水平向右为正方向,对$P$、$Q$分别应用动量定理,对$P$有$-{{F}_{P安}}\cdot t=m{{v}_{{P}}}-m{{v}_{0}}$
对$Q$有${{F}_{Q安}}\cdot t=M{{v}_{Q}}$
其中${{F}_{{P安}}}=3{{F}_{{Q安}}}$
整理得$m{{v}_{0}}-m{{v}_{{P}}}=3M{{v}_{{Q}}}$
两棒最后匀速时,电路中无电流,此时回路总电动势为零,必有$3BL{v}_{P}=BL{v}_{Q}$
即${{v}_{{Q}}}=3{{v}_{{P}}}$
联立解得${{v}_{{P}}}=\dfrac{2}{19}\;\rm {m/s}$,$\rm B$正确;
$\rm C$.在$Q$加速过程中根据动量定理有$\sum BiL\Delta t=M{{v}_{{Q}}}-0$
又电荷量$Q=\sum i\Delta t$
解得$q=\dfrac{60}{19}{\;\rm C}$,$\rm C$正确;
$\rm D$.根据$q=\dfrac{\Delta \Phi }{2R}=\dfrac{B\Delta S}{2R}$
代入数据解得$\Delta S=\dfrac{240}{19}{{\;\rm {m}}^{2}}$,$\rm D$错误。
故选:$\rm B$。
| 双棒模型题目答案及解析(完整版)
