如图所示，水平面内固定有两根平行的光滑长直金属导轨，导轨间距为$l$，电阻不计。整个装置处于两个磁感应强度大小均为$B$、方向相反的竖直方向匀强磁场中，虚线为两磁场的分界线，质量为$m$、导轨间电阻为$R$的导体棒$MN$和质量为$2m$、导轨间电阻为$2R$的导体棒$PQ$静置于图示的导轨上（两棒始终与导轨垂直且接触良好）。现使$MN$棒获得一个大小为$v_{0}$、方向水平向左的初速度，则在此后的整个运动过程中$(\qquad)$

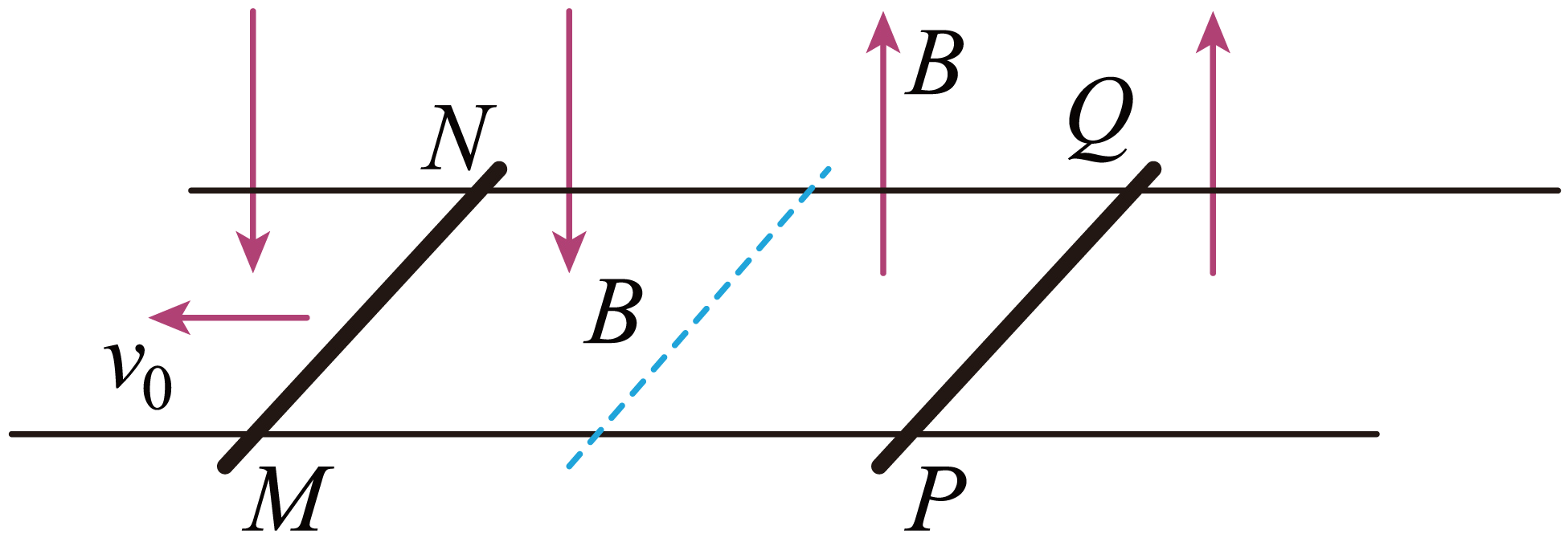
两棒受到的安培力冲量大小相等方向相反

两棒最终的速度大小均为$\\dfrac{v_{0}}{3}$

$MN$棒产生的焦耳热为$\\dfrac{mv_{0}^{2}}{4}$

$MN$棒克服安培力做功的功率等于安培力对$PQ$棒做功的功率与两棒总发热功率之和

$\rm A$．根据右手定则可知，从上往下看。感应电流方向为逆时针，根据左手定则可知，两棒受到的安培力方向均为水平向右，大小相等，即两棒受到的安培力冲量大小相等方向相同，$\rm A$错误；

$\rm B$．根据上述可知，$MN$向左做减速运动，$PQ$向右做加速运动，当速度大小相等时，根据右手定则可知，回路总电动势为$0$，感应电流为$0$，此后两棒做匀速直线运动，对$MN$棒有$-B\overline{I}l\Delta t=mv_{1}-mv_{0}$

对$PQ$棒有$B\overline{I}l\Delta t=2mv_{1}$

解得$v_{1}=\dfrac{v_{0}}{3}$

$\rm B$正确；

$\rm C$．根据上述，回路产生的总焦耳热为$Q=\dfrac{1}{2}mv_{0}^{2}-\dfrac{1}{2}mv_{1}^{2}-\dfrac{1}{2} \times 2mv_{1}^{2}$

则$MN$棒产生的焦耳热为$Q_{MN}=\dfrac{1}{3}Q$

解得$Q_{MN}=\dfrac{mv_{0}^{2}}{9}$

$\rm C$错误；

$\rm D$．根据功能关系可知，上述过程中，安培力对$MN$棒做负功，将$MN$棒的动能转化为电能，安培力对$PQ$棒做正功，将一部分电能转化为动能，电流通过电阻，一部分电能又转化为焦耳热，可知$MN$棒克服安培力做功的功率等于安培力对$PQ$棒做功的功率与两棒总发热功率之和，$\rm D$正确。

故选：$\rm BD$。