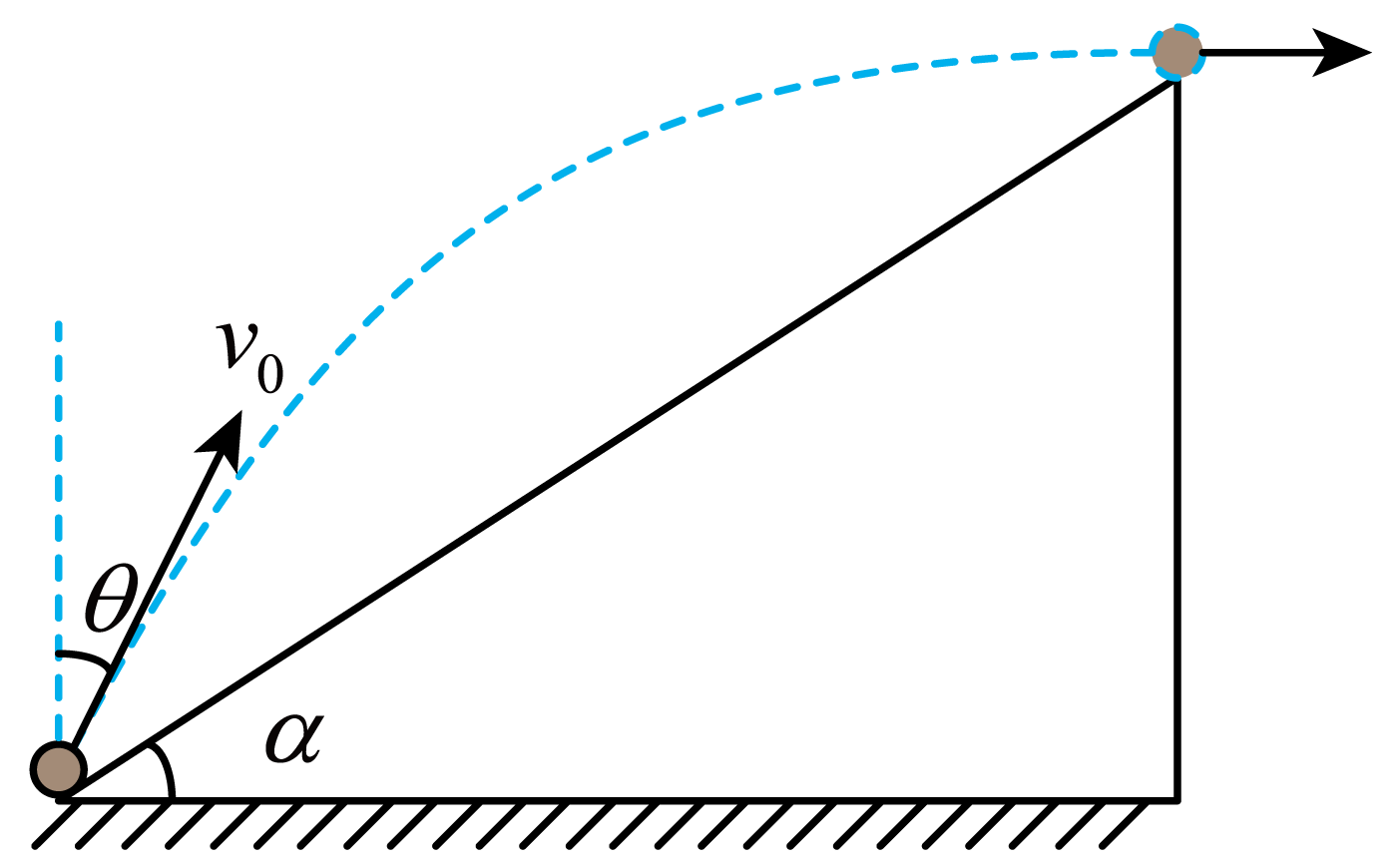
如图所示，将小球由一倾角为$\alpha$的固定斜面底端以与竖直方向夹角$\theta=30^\circ $的速度$v_{0}$斜向上抛出，小球恰好以水平速度经过斜面顶端。小球可视为质点，不考虑空气阻力，已知重力加速度为$g$。下列说法正确的是$(\qquad)$

小球经过斜面顶端时的速度大小为$\\dfrac{\\sqrt{3}v_{0}}{2}$

小球由斜面底端运动至顶端的时间为$\\dfrac{\\sqrt{3}v_{0}}{2g}$

斜面的高度为$\\dfrac{3v_{0}^{2}}{4g}$

斜面的倾角$\\alpha=30^\\circ $

$\rm A$．小球恰好以水平速度经过斜面顶端，小球在水平方向做匀速直线运动，则小球经过斜面顶端时的速度$v=v_{x}=v_{0}\sin\theta=\dfrac{v_{0}}{2}$，故$\rm A$错误；

$\rm BC$．小球恰好以水平速度经过斜面顶端，可知斜面顶端是小球斜抛的最高点，则小球由斜面底端运动至顶端的时间$t=\dfrac{v_{0}\cos30{^\circ}}{g}=\dfrac{\sqrt{3}v_{0}}{2g}$

斜面的高度$h=\dfrac{\left( v_{0}\cos30{^\circ} \right)^{2}}{2g}=\dfrac{3v_{0}^{2}}{8g}$

故$\rm B$正确，$\rm C$错误；

$\rm D$．斜面的倾角满足$\tan\alpha=\dfrac{h}{x}=\dfrac{h}{v_{x}t}=\dfrac{\dfrac{3v_{0}^{2}}{8g}}{\dfrac{v_{0}}{2} \times \dfrac{\sqrt{3}v_{0}}{2g}}=\dfrac{\sqrt{3}}{2} \gt \dfrac{\sqrt{3}}{3}$

可得斜面的倾角$\alpha$大于$30^\circ $，故$\rm D$错误。

故选：$\rm B$。