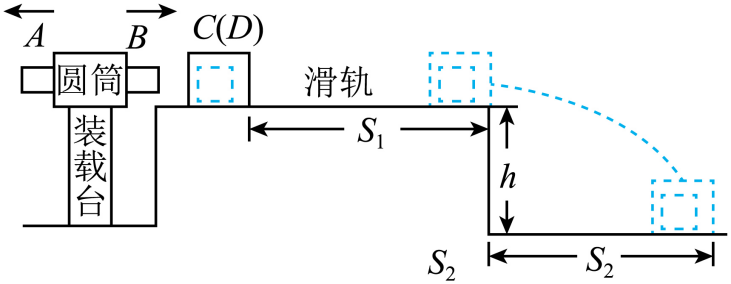
如图，某爆炸能量测量装置由装载台和滑轨等构成，$C$是可以在滑轨上运动的标准测量件，其规格可以根据测量需求进行调整。滑轨安装在高度为$h$的水平面上。测量时，将弹药放入装载台圆筒内，两端用物块$A$和$B$封装，装载台与滑轨等高。引爆后，假设弹药释放的能量完全转化为$A$和$B$的动能。极短时间内$B$嵌入$C$中形成组合体$D$，$D$与滑轨间的动摩擦因数为$\mu $。$D$在滑轨上运动$S_{1}$距离后抛出，落地点距抛出点水平距离为$S_{2}$，根据$S_{2}$可计算出弹药释放的能量。某次测量中，$A$、$B$、$C$质量分别为$3m$、$m$、$5m$，$S_{1}=\dfrac{h}{\mu}$，整个过程发生在同一竖直平面内，不计空气阻力，重力加速度大小为$g$。则$(\qquad)$

$D$的初动能与爆炸后瞬间$A$的动能相等

$D$的初动能与其落地时的动能相等

弹药释放的能量为$36mgh\\left( 1+\\dfrac{S_{2}^{2}}{4h^{2}} \\right)$

弹药释放的能量为$48mgh\\left( 1+\\dfrac{S_{2}^{2}}{4h^{2}} \\right)$

$\rm A$．爆炸后，$AB$组成的系统动量守恒，即$3mv_{1}=mv_{2}$

$B$与$C$碰撞过程动量守恒$mv_{2}=6mv$

联立解得$v=0.5v_{1}$。

爆炸后瞬间$A$的动能$E_{{kA}}=\dfrac{1}{2} \cdot 3m \cdot {v_{1}}^{2}$

$D$的初动能$E_{{kD}}=\dfrac{1}{2} \cdot 6m \cdot \left( 0.5v_{1} \right)^{2}$

两者不相等，故$\rm A$错误；

$\rm B$．$D$水平滑动过程中摩擦力做功为$W_{{f}}=-\mu \cdot 6mg \cdot S_{1}=- \mu \cdot 6mg \cdot \dfrac{h}{\mu}=- 6mgh$

做平抛运动过程中重力做的功为$W_{G}=6mgh$

故$D$从开始运动到落地瞬间合外力做功为$0$，根据动能定理可知$D$的初动能与其落地时的动能相等，故$\rm B$正确；

$\rm CD$．$D$物块平抛过程有$h=\dfrac{1}{2}gt^{2}$，$S_{2}=\dfrac{v_{0}}{t}$

联立可得$v_{0}=S_{2}\sqrt{\dfrac{g}{2h}}$

$D$水平滑动过程中根据动能定理有$- 6mgh=\dfrac{1}{2} \cdot 6mv_{0}^{2}-\dfrac{1}{2} \cdot 6mv^{2}$

化简得$v^{2}=\dfrac{S_{2}^{2}g}{2h}+2gh$

弹药释放的能量完全转化为$A$和$B$的动能，则爆炸过程的能量为$E=\dfrac{1}{2} \cdot 3mv_{1}^{2}+\dfrac{1}{2} \cdot mv_{2}^{2}=24mv^{2}=24\left( \dfrac{S_{2}^{2}g}{2h}+2gh \right)=48mgh\left( 1+\dfrac{S_{2}^{2}}{4h^{2}} \right)$

故$\rm C$错误，$\rm D$正确。

故选：$\rm BD$。