如图所示，$O$处为地心，卫星$1$环绕地球做匀速圆周运动，卫星$2$环绕地球运行的轨道为椭圆，两轨道不在同一平面内。已知圆轨道的直径等于椭圆轨道的长轴，且地球位于椭圆轨道的一个焦点上，引力常量为$G$，地球的质量为$M$，卫星$1$的轨道半径为$R$，卫星$1$的运转速度为$v_{0}$，关系为$OQ=1.5R$。下列说法正确的是$(\qquad)$

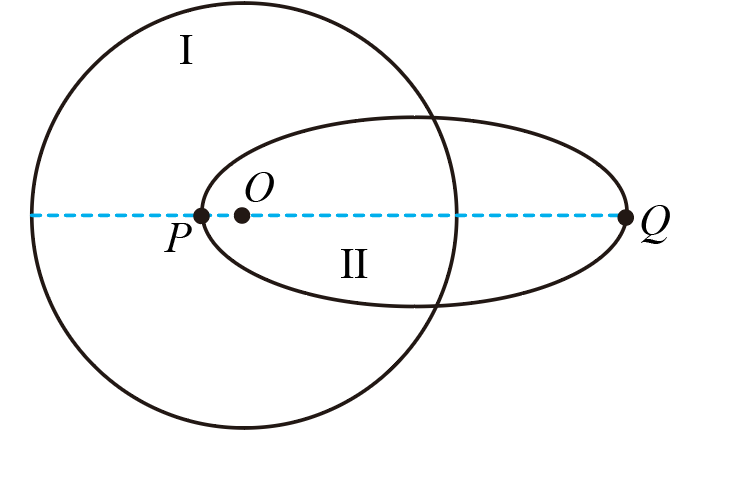
卫星$1$的运行周期大于卫星$2$的运行周期

如果卫星$1$的加速度为$a$，卫星$2$在$P$点的加速度为$a_{p}$，则$a \\gt a_{p}$

卫星$2$在$Q$点的速度$v_{Q}=\\sqrt{\\dfrac{2GM}{3R}}$

卫星$2$在$P$、$Q$点的速度大小关系为$v_{p} \\gt v_{0} \\gt v_{Q}$

$\rm A$．题意可知卫星$2$的轨道半长轴为$R$，根据开普勒第三定律$\dfrac{a^{3}}{T^{2}}=k$

由于卫星$1$的半径等于卫星$2$的半长轴，所以卫星$1$的运行周期等于卫星$2$的运行周期，故$\rm A$错误；

$\rm B$．设卫星质量为$m$，则有$G\dfrac{Mm}{r^{2}}=ma$

解得$a=G\dfrac{M}{r^{2}}$

由于$P$点距离中心天体较近，所以$a \lt a_{P}$

故$\rm B$错误；

$\rm C$．若卫星$2$在$OQ$为半径的轨道上做匀速圆周运动，万有引力提供向心力$G\dfrac{Mm}{(1.5R)^{2}}=m\dfrac{v^{2}}{1.5R}$

解得$v=\sqrt{\dfrac{2GM}{3R}}$

由于卫星在椭圆轨道的$Q$点要做近心运动，所以$v_{Q} \lt \sqrt{\dfrac{2GM}{3R}}$

故$\rm C$错误；

$\rm D$．若卫星在$P$点做半径为$R$的圆周运动，根据$v=\sqrt{\dfrac{GM}{r}}$

易知卫星在$P$点做半径为$R$的圆周运动的速度$v_{1}$大于$v_{0}$（$v_{1} \gt v_{0}$），由于卫星在圆轨道的$P$点要做离心运动，则有$v_{p} \gt v_{1} \gt v_{0}$

同理，若卫星在$Q$点做半径为$1.5R$的圆周运动，根据$v=\sqrt{\dfrac{GM}{r}}$

易知卫星在$Q$点做半径为$1.5R$的圆周运动的速度$v_{2}$小于$v_{0}$（$v_{2} \lt v_{0}$），由于卫星在圆轨道的$Q$点要做近心运动，则有$v_{0} \gt v_{2} \gt v_{Q}$

综合以上可知$v_{p} \gt v_{0} \gt v_{Q}$

故$\rm D$正确。

故选：$\rm D$。