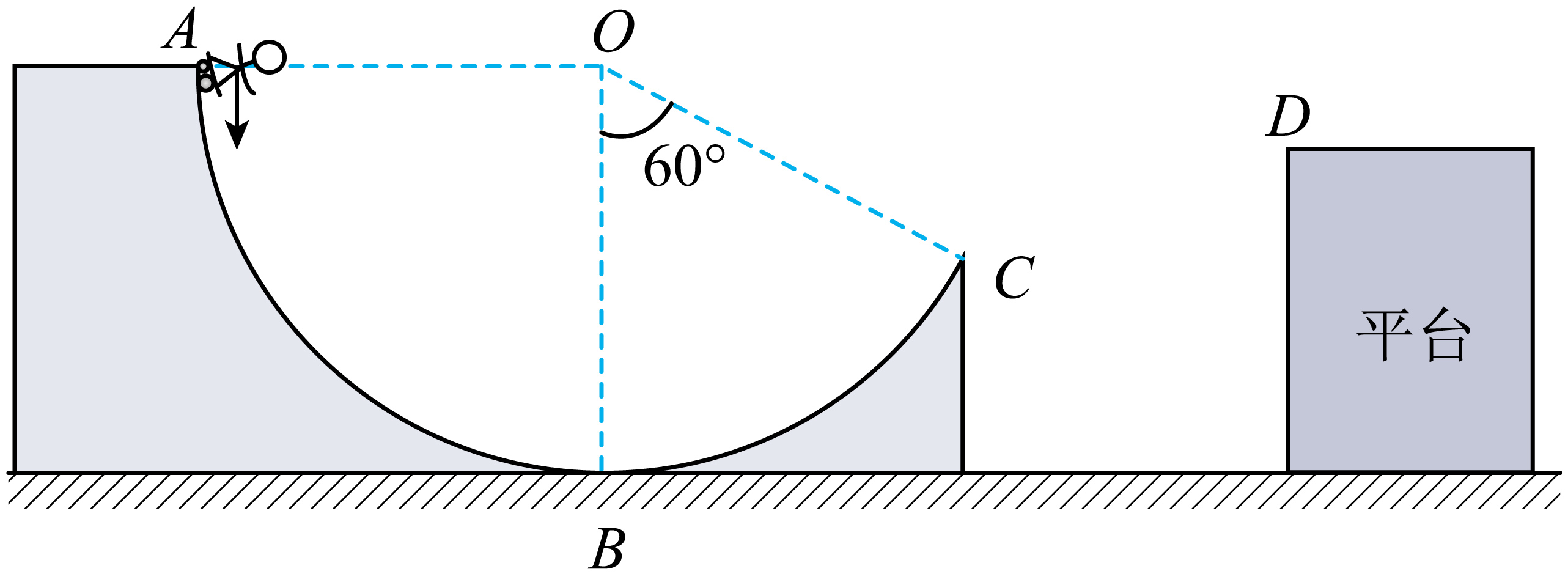
运动员从$C$点滑出时的速度大小；

$\\dfrac{2}{3}\\sqrt{3gR}$

设运动员从$C$点滑出的速度大小为$v_{C}$，运动员从$C$点滑出后，竖直上升的高度$h=R\cos 60^\circ $

竖直方向分运动$(v_{C}\sin 60^\circ )^{2}=2gh$

解得$v_{C}=\dfrac{2}{3}\sqrt{3gR}$

运动员和轮滑鞋一起在$B$点对轨道的压力；

$\\dfrac{10}{3}mg$，方向竖直向下

设运动员到$B$点时速度大小为$vB$，从$B$到$C$，根据机械能守恒$- mg(R-R\cos 60{^\circ})=\dfrac{1}{2}mv_{C}^{2}-\dfrac{1}{2}mv_{B}^{2}$

在$B$点，根据牛顿第二定律有$F-mg=m\dfrac{v_{B}^{2}}{R}$

解得$F=\dfrac{10}{3}mg$

根据牛顿第三定律，运动员和轮滑鞋一起在$B$点对轨道的压力大小$F'=F=\dfrac{10}{3}mg$

方向竖直向下

平台$D$点离圆弧轨道$C$点的水平距离。

$\\dfrac{\\sqrt{3}}{2}R$

运动员从$C$点滑出后，上升的过程有$v_{C}\sin 60^\circ =gt_{1}$

设下降的时间为$t_{2}$，则$\dfrac{1}{8}R=\dfrac{1}{2}gt_{2}^{2}$

则$D$点与$C$点的水平距离$s=v_{C}\cos 60{^\circ}(t_{1}+t_{2})=\dfrac{\sqrt{3}}{2}R$