如图所示，$AB$是位于竖直平面内的四分之一圆弧形的光滑绝缘轨道，半径$R=0.5\;\rm m$，$OA$水平，轨道下端点$B$与水平粗糙绝缘轨道平滑连接，整个空间分布有水平向左的匀强电场，电场强度$E=1 \times 10^{4}\;\rm N/C$。有一质量$m=0.1\;\rm kg$、电荷量$q=+7.5 \times 10^{-5}\;\rm C$的小滑块（可视为质点）从水平轨道上某点$P$由静止释放，恰好能运动到$A$点。若已知滑块与水平轨道间的动摩擦因数$\mu =0.05$，取$g=10\;\rm m/s^{2}$，则下列说法正确的是$(\qquad)$

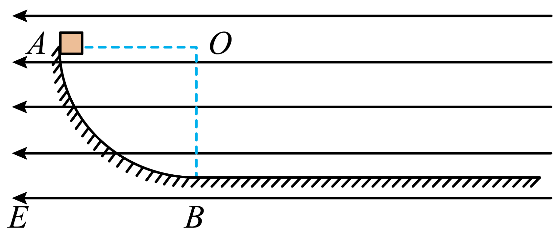
释放点$P$与$B$的水平距离为$\\dfrac{5}{28}\\;\\text{m}$

滑块第一次经过$B$点时，对轨道的压力大小为$1.5\\;\\rm N$

滑块最终停在$B$处

滑块在粗糙段轨道上的总路程为$\\dfrac{75}{28}\\;\\text{m}$

$\rm A$．设释放点$P$与$B$的水平距离为$x$，对滑块从$P$到$A$的过程，根据动能定理可得$qE(x+R)-\mu mgx-mgR=0$，代入数据解得$x=\dfrac{5}{28}\;\text{m}$，故$\rm A$正确；

$\rm B$．对滑块从$B$到$A$的过程，根据动能定理可得$qER-mgR=0-\dfrac{1}{2}mv_{B}^{2}$，在$B$点，根据牛顿第二定律可得$F_{\text{N}}-mg=m\dfrac{v_{B}^{2}}{R}$，联立解得$F_{N}=1.5\;\rm N$，根据牛顿第三定律可知滑块对轨道的压力大小为$1.5\;\rm N$，故$\rm B$正确；

$\rm C$．因为$qE=7.5\times10^{-5}\times1\times10^{4}\;\rm N=0.75\;\rm N$，$\mu mg=0.05\times0.1\times10\;\rm N=0.05\;\rm N$，则有$qE\gt\mu mg$，所以滑块不会最终停在$B$处，故$\rm C$错误；

$\rm D$．滑块最终会在$B$点上方的圆弧轨道上来回运动，且在$B$点时速度为$0$，设滑块在粗糙段轨道上的总路程为$s_{总}$，对滑块从$P$到最终状态的过程，根据动能定理可得$qEx-\mu mgs_{总}=0$，解得$s_{总}=\dfrac{75}{28}\;\text{m}$，故$\rm D$正确。

故选：$\rm ABD$。