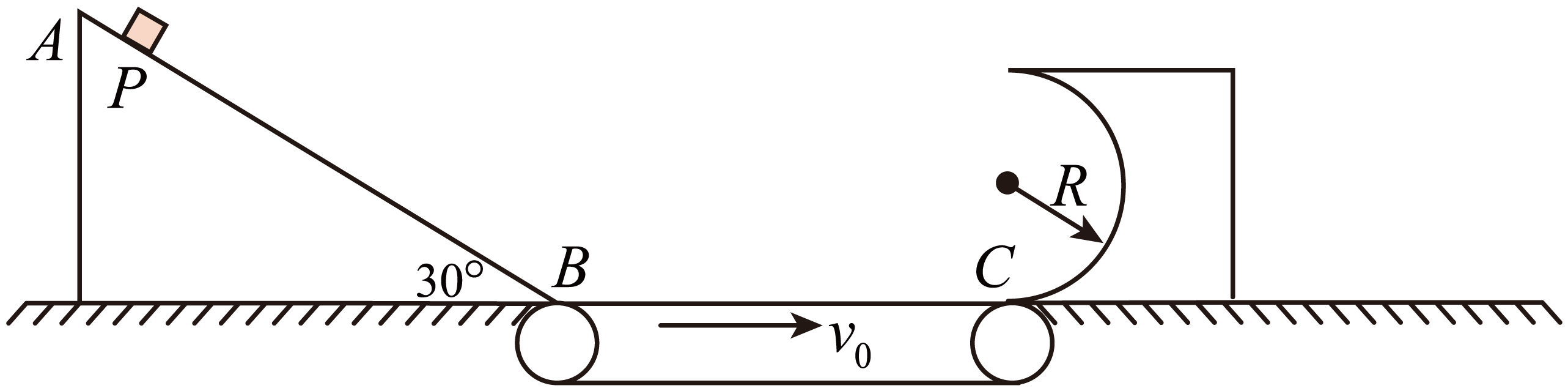
滑到$B$点处的速度大小；

$4\\;\\rm m/s$

滑块从$P$点到$B$点由动能定理$mgL\sin 30{^\circ}=\dfrac{1}{2}mv^{2}$

解得到达$B$点的速度$v=4\;\rm m/s$

从$B$点运动到$C$点过程中摩擦力对其做的功；

$0.9\\;\\rm J$

物块滑上传送带后做加速运动直到与传送带共速，摩擦力对其做的功$W_{f}=\dfrac{1}{2}mv_{0}^{2}-\dfrac{1}{2}mv^{2}= 0.9\;\rm \text{J}$

在传送带上滑动过程中产生的滑痕长度；

$0.2m$

物块在传送带上加速运动的加速度为$a=\mu g=2.5\;\rm m/s^{2}$

加速到共速时用时间$t=\dfrac{v_{0}-v}{a}=\dfrac{5-4}{2.5}\;\rm \text{s}=0.4\;\rm \text{s}$

在传送带上滑动过程中产生的滑痕长度$\Delta x=v_{0}t-\dfrac{v_{0}+v}{2}t=0.2\;\rm \text{m}$

即将离开圆弧轨道最高点的瞬间，受到轨道的压力大小。

$3\\;\\rm N$

从滑块开始进入圆弧槽到到达圆弧槽最高点由水平方向动量守恒和能量关系可知$mv_{0}=mv_{1}+Mv_{2}$，$\dfrac{1}{2}mv_{0}^{2}=\dfrac{1}{2}mv_{1}^{2}+ \dfrac{1}{2}Mv_{2}^{2}+2mgR$

联立解得$v_{1}=-2.2\;\rm m/s$，$v_{2}=0.8\;\rm m/s$

（另一组$v_{1}=3.2\;\rm m/s$，$v_{2}=0.2\;\rm m/s$，因不合实际舍掉）

对滑块在最高点时由牛顿第二定律$F+mg=m\dfrac{{(v_{2}-v_{1})}^{2}}{R}$

解得$F=3\;\rm N$