高中 | 洛伦兹力 题目答案及解析
稿件来源:高途
高中 | 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
如图所示,在绝缘水平面上方,相距为$L$的竖直边界$MO$、$NA$之间存在水平向左的匀强电场,场强大小为$E_{1}$。边界$NA$右侧有一直角三角形区域$ACD$,区域内存在垂直纸面向外的匀强磁场和大小为$E_{2}=\dfrac{mg}{q}$、方向竖直向下的匀强电场。在边界$MO$上的$O$点静止释放一个质量为$m$、电量大小为$q$的带电小球(大小忽略不计),小球从$A$点进入三角形场区,最终从$AD$边界上的$P$点离开。已知$AP$间的距离为$d$,$∠DAC=30^\circ$,不计一切摩擦。
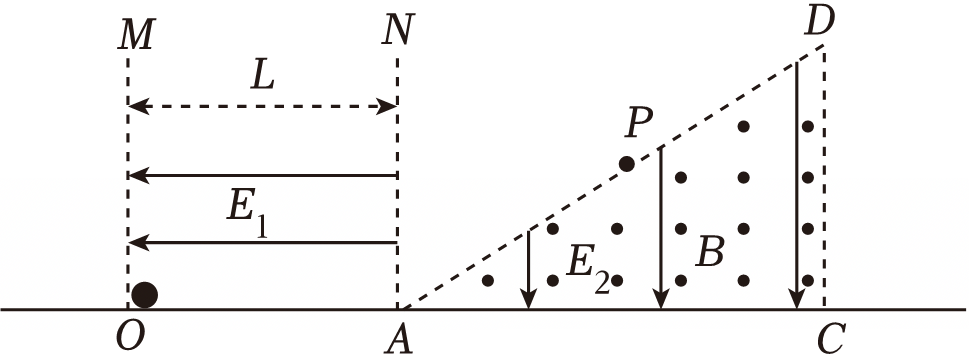
求$ACD$区域内的磁感应强度大小;
$\\dfrac{1}{d}\\sqrt{\\dfrac{2mE_{1}L}{q}}$
"]]小球在电场$E_{1}$中加速,有$qE_{1}L= \dfrac{1}{2}mv_{0}^{2}$
小球进入$ACD$场区时,有$qE_{2}=mg$
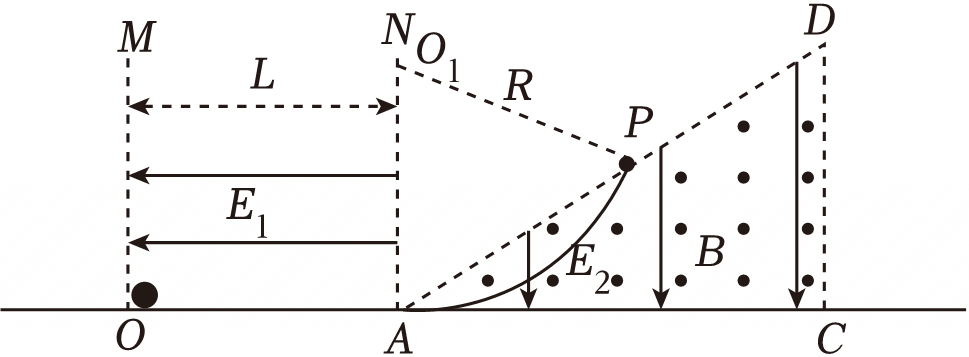
小球做匀速圆周运动,运动轨迹如图,由几何关系得轨道半径为$R=d$
根据牛顿第二定律,有$qv_{0}B=m\dfrac{{v_{0}}^{2}}{R}$
解得$B= \dfrac{1}{d}\sqrt{\dfrac{2mE_{1}L}{q}}$
求小球从$O$运动到$P$所用时间。
$\\sqrt{\\dfrac{2mL}{qE_{1}}}+\\dfrac{\\pi d}{3}\\sqrt{\\dfrac{m}{2qE_{1}L}}$
解:小球在加速场中运动,有$qE_{1}=ma$
$L=\\dfrac{1}{2}a{t_{1}}^{2}$
小球在磁场中做圆周运动,由图可知小球转过的圆心角为$60^\\circ$,有$T= \\dfrac{2\\pi R}{v_{0}}$
小球在磁场中做圆周运动时间$t_{2}=\\dfrac{1}{6}T$
且$t=t_{1}+t_{2}$
联立各式,解得$t= \\sqrt{\\dfrac{2mL}{qE_{1}}}+\\dfrac{\\pi d}{3}\\sqrt{\\dfrac{m}{2qE_{1}L}}$
"]]高中 | 洛伦兹力题目答案及解析(完整版)
