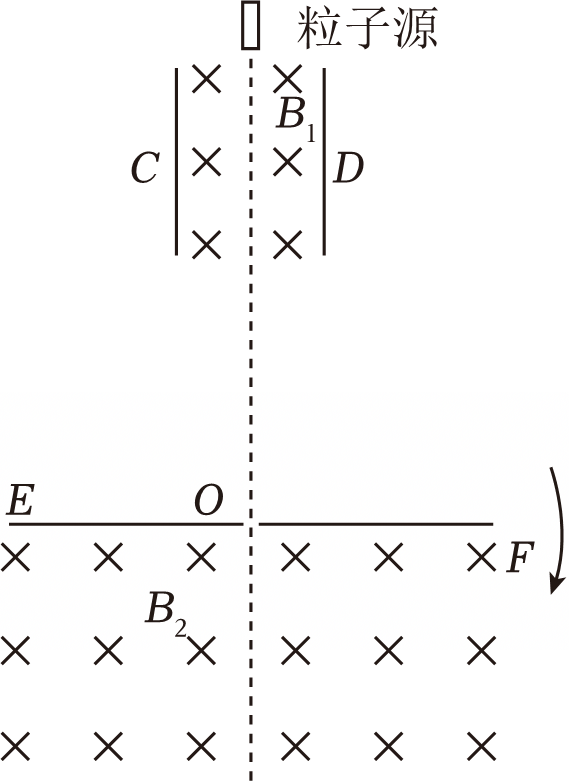
判断$C$、$D$板哪个电势高，并求粒子的速度。

右侧极板$D$的电势高；粒子速度为$\\dfrac{U}{B_{1}d}$

由粒子可以打在$OF$中点，结合左手定则，可知粒子带正电；

根据左手定则，则粒子在$CD$间受到水平向右的洛伦兹力，为保持粒子能沿竖直的虚线运动，故电场力应与洛伦兹力等大反向，

即粒子受水平向左的电场力，电场方向从右向左，即右侧极板$D$的电势高；

且电场力和洛伦兹力满足：$q\dfrac{U}{d}=qB_{1}v$，得：$v=\dfrac{U}{B_{1}d}$

求该粒子的比荷；

粒子的比荷为$\\dfrac{2U}{B_{1}B_{2}dL}$

粒子在$EF$板下方做匀速圆周运动时，恰好击中$OF$中点，进入磁场时与$EF$垂直，故出磁场时也与$EF$垂直，轨迹如图：

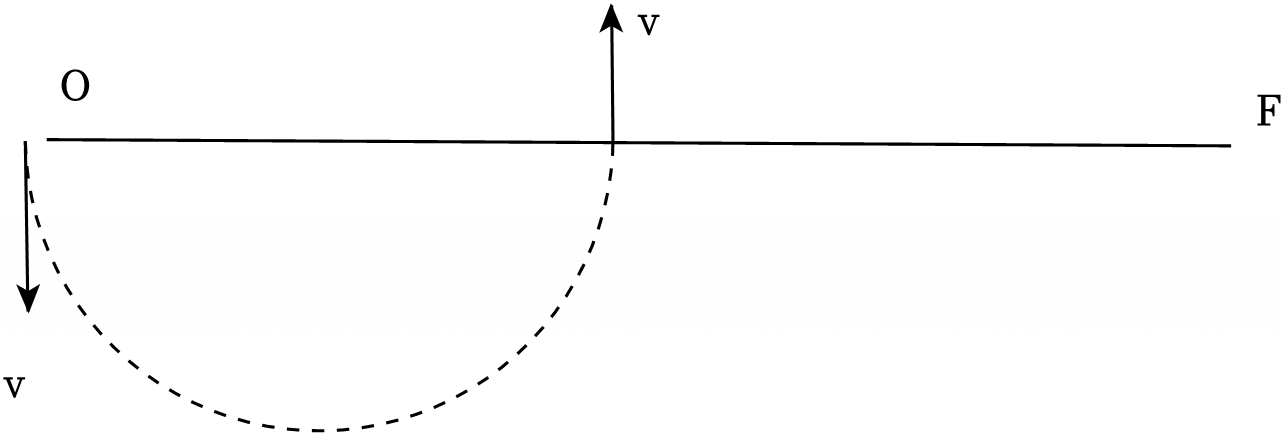
由图可知其半径为$2r=\dfrac{OF}{2}=\dfrac{1}{2} \times \dfrac{EF}{2}=\dfrac{1}{2} \times \dfrac{4L}{2}=L$，即半径为：$r=\dfrac{L}{2}$，

由洛伦兹力提供向心力：$qB_{2}v=m\dfrac{v^{2}}{r}$，解得：$\dfrac{q}{m}=\dfrac{2U}{B_{1}B_{2}dL}$

$EF$板绕过$O$点、垂直于纸面的轴顺时针转动$180^\circ$过程中，分别求出$OE$、$OF$上被粒子击中的范围。

粒子打到$OE$板上的范围为：从$OE$的中点，到$E$点之间的范围内；打在$OF$板上的范围为：从$O$点开始，与$O$距离为$L$的范围内

$EF$板转动后，在粒子打到板上前，在磁场中的运动轨迹依然是圆周运动的轨迹，与（$2$）中的轨迹重合；

由几何关系可知在极板转过角度$0\leqslant \theta\leqslant 90^\circ$的过程中，打在极板上的位置如图所示：

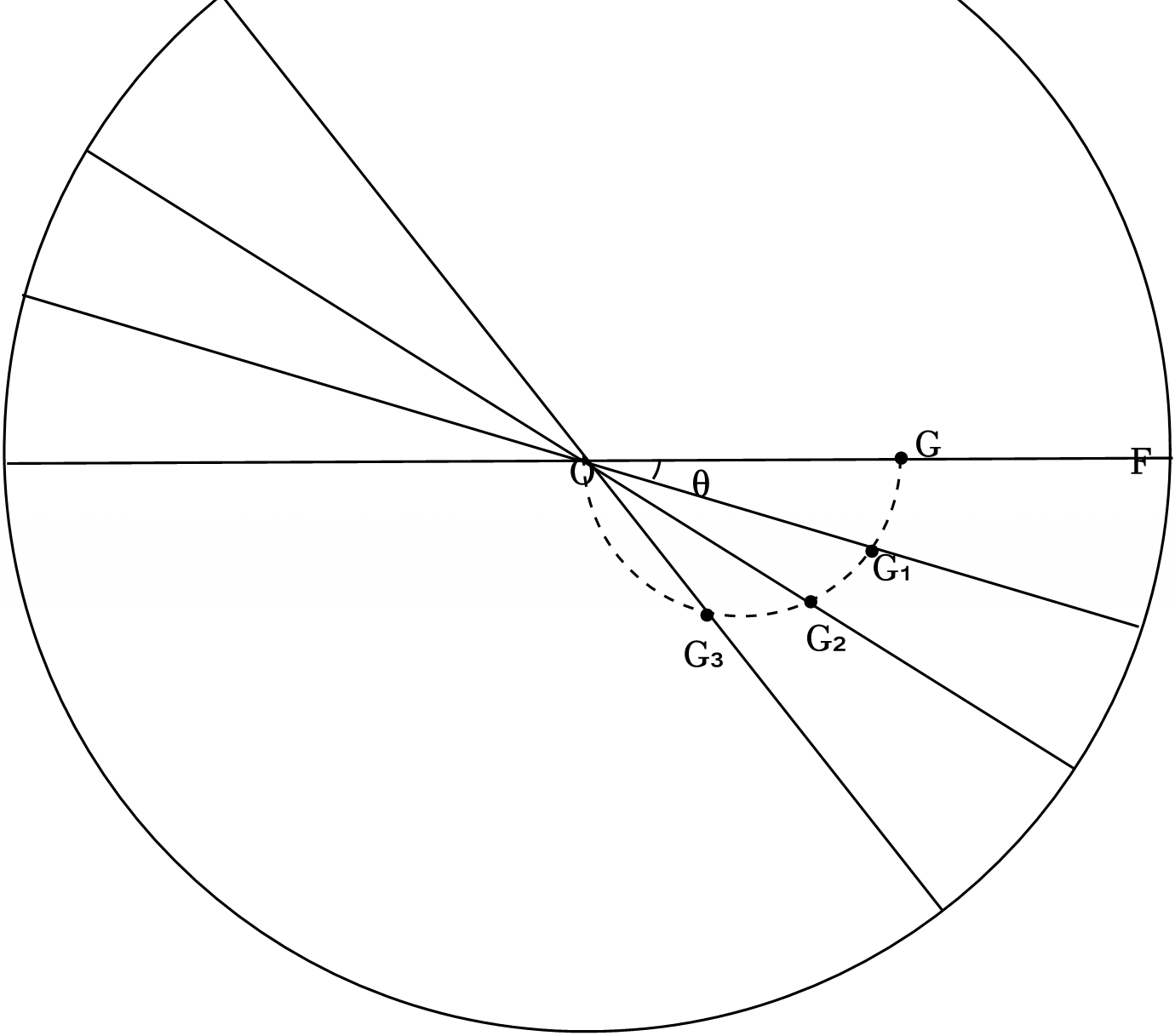
即打在板上的位置越来越靠近$O$点，即打在$OF$板上的范围为：从$O$点开始，与$O$距离为$L$的范围内；

由几何关系可知在极板转过角度$90^\circ≤\theta≤180^\circ$的过程中，打在极板上的位置如图所示：

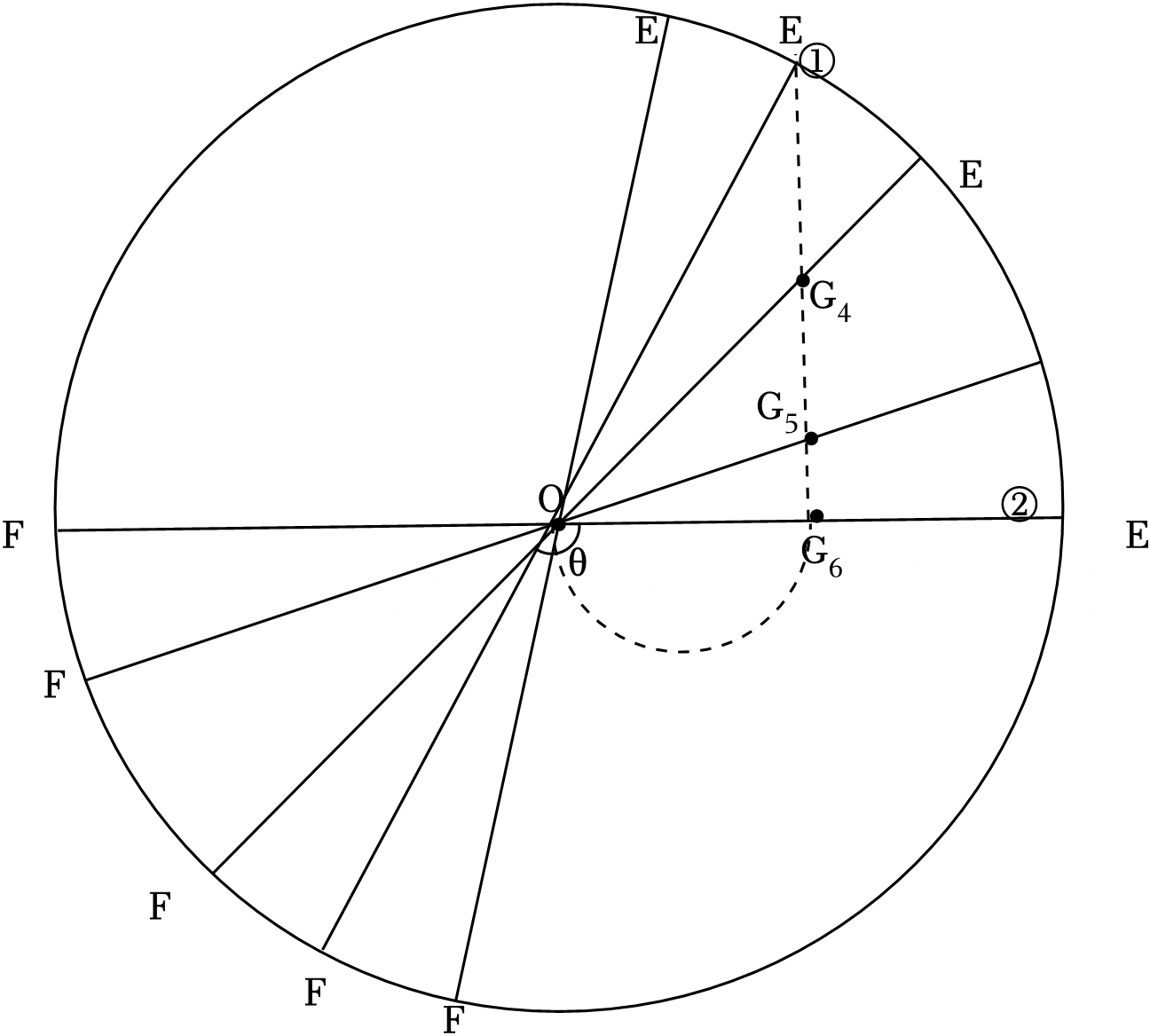
在极板转到①位置前，粒子打不到板上；

在极板转到①位置时，粒子刚好打到极板的$E$点上；

在极板转到①位置后，粒子打在板上的位置会越来越靠近$O$点，直到$\theta=180^\circ$时，即极板转到②位置时，粒子打到$OE$的中点；

即粒子打到$OE$板上的范围为：从$OE$的中点到$E$点之间的范围内。