如图所示，质量为$m$、电荷量为$+q$的粒子从静止开始经加速电压$U$加速后，从三维直角坐标系的原点$O$处沿不同方向射入匀强磁场，磁感应强度大小为$B$、方向沿$z$轴正方向。已知加速电压$U$调节范围为$U_{0}\leqslant U\leqslant 3U_{0}$，其中$U_{0}= \dfrac{qB^{2}L^{2}}{8m}$。$x$轴上距离$O$点$1.5L$处有一长为$L$的吸收板，吸收板接地，粒子打在板上即被吸收。不计粒子重力，下列说法正确的是$(\qquad)$

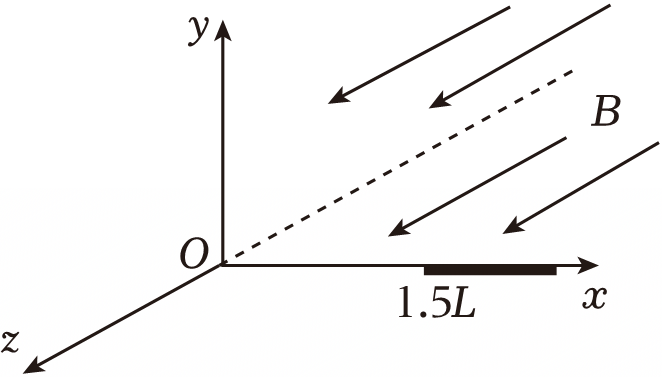
当粒子沿$y$轴正方向射入磁场时，调节$U$，板上有粒子击中的长度为$\\left(\\sqrt{3}-\\dfrac{3}{2}\\right)L$

当$U=3U_{0}$，粒子从$O$点射入$xOy$平面$x\\gt 0$、$y\\gt 0$的区域，速度方向在$0\\sim 90^\\circ$均匀变化，且沿各方向发射的粒子数目相等，则击中吸收板的粒子占粒子总数的$50\\%$

当$U=U_{0}$，$t=0$时刻，粒子从$O$点射入$yOz$平面$y\\gt 0$、$z\\lt 0$的区域，且速度方向与$y$轴正方向夹角为$30^\\circ$，粒子与$z$轴距离最大时的时间为$t_{1}=n\\dfrac{\\pi m}{qB}(n=1,2,3⋯⋯)$

当$U=2U_{0}$，粒子从$O$点射入$yOz$平面$y\\gt 0$、$z\\lt 0$的区域，且速度方向与$y$轴正方向夹角为$45^\\circ$，则经过$t_{2}= \\dfrac{3\\pi m}{2qB}$时粒子的坐标为$\\left(\\dfrac{L}{2},- \\dfrac{L}{2},- \\dfrac{3}{4}\\pi L\\right)$

$\rm A$．粒子经加速电压$U$后，由动能定理可知$qU=\dfrac{1}{2}mv^{2}$

速度$v=\sqrt{\dfrac{2qU}{m}}$

代入磁场中半径公式$r=\dfrac{mv}{qB}$

可求得粒子的轨迹半径与电压的关系，当$U=U_{0}=\dfrac{qB^{2}L^{2}}{8m}$时，半径$r_{1}=\dfrac{L}{2}$

$U=2U_{0}$ 时，半径$r_{2}= \dfrac{\sqrt{2}L}{2}$

$U=3U_{0}$时，半径$r_{3}=\dfrac{\sqrt{3}L}{2}$

当粒子沿$y$轴正方向射入磁场时，粒子在$xOy$平面偏转半个圆周打在$x$轴上，当加速电压为$3U_{0}$时粒子打中板上位置最远，为$\sqrt{3}L$，因此打中板长度为$\left(\sqrt{3}-\dfrac{3}{2}\right)L$

故$\rm A$正确；

$\rm B$．当$U=3U_{0}$、粒子射向$xOy$平面，恰好打在板上的临界情况如图所示：

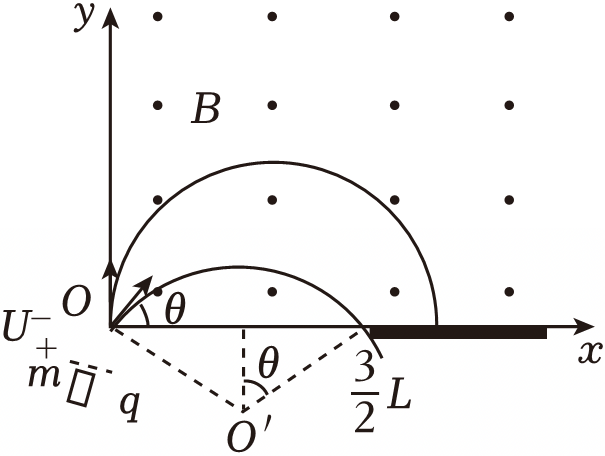
由几何关系可知：$\sin\theta=\dfrac{\dfrac{3}{4}L}{\dfrac{\sqrt{3}}{2}L}=\dfrac{\sqrt{3}}{2}$

$\theta=60^\circ$

则击中吸收板的粒子占粒子总数的比例为$\dfrac{90{^\circ}-60{^\circ}}{90{^\circ}} \times 100\%=33\%$

故$\rm B$错误；

$\rm C$．当$U=U_{0}$，粒子射向$yOz$平面，速度方向与$y$轴正方向夹$30^\circ$时，粒子的运动轨迹如下图所示：

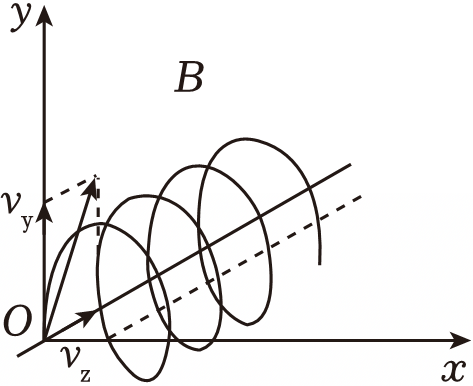
将速度分解为沿$y$轴方向的$v_{y}$和沿$z$轴方向的$v_{1}$，则粒子在$z$轴方向以$v_{1}$分速度做匀速直线运动，在$xOy$平面以$v_{y}$分速度做匀速圆周运动，故当粒子运动半周期的奇数倍时粒子离$z$轴最远，由$T=\dfrac{2\pi m}{qB}$可知，粒子与$z$轴距离最大时的时间为$t_{1}=n\dfrac{\pi m}{qB}(n=1,3,5\cdots\cdots)$

故$\rm C$错误；

$\rm D$．当$U=2U_{0}$，粒子速度方向与$xOy$平面和$z$坐标轴夹角均为$45^\circ$时，初速度大小为$v_{0}=\dfrac{\sqrt{2}qBL}{2m}$

将其分解为$z$轴方向分速度$v_{Z}=\dfrac{qBL}{2m}$和$xOy$平面分速度$v_{xOy}=\dfrac{qBL}{2m}$粒子在$z$轴方向以$v_{1}$分速度做匀速直线运动，在$xOy$平面以$v_{AOy}$分速度做匀速圆周运动，则经过$t_{2}=\dfrac{3\pi m}{2qB}$时粒子的坐标为$\left(\dfrac{L}{2},-\dfrac{L}{2},-\dfrac{3}{4}\pi L\right)$

故$\rm D$正确。

故选：$\rm AD$。