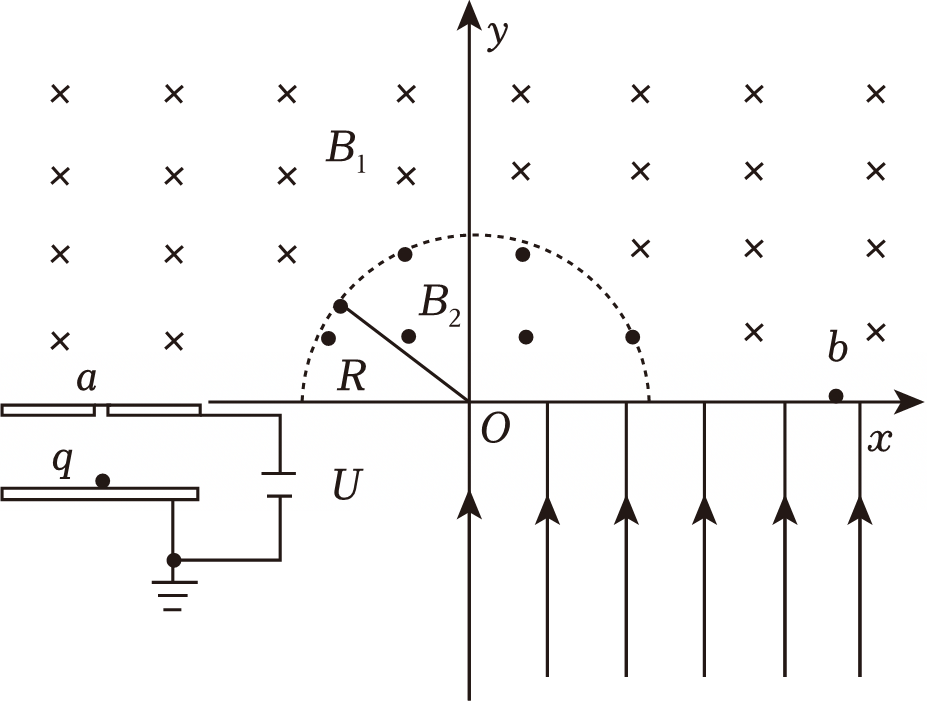
若粒子未进入半圆形区域内磁场，加速电场的电压多大；

若粒子未进入半圆形区域内磁场，加速电场的电压为$\\dfrac{2qB_{1}^{2}R^{2}}{m}$

设粒子经过$a$点的速度为$v$，加速电场的加速电压为$U$，根据动能定理可得：

$qU= \dfrac{1}{2}mv^{2}$

当粒子未进入半圆形区域内磁场时，粒子在磁场$B_{1}$中直接从$a$点到$b$点，其运动轨迹恰好为半个圆周，此时粒子运动的轨道半径为：$r=2R$

根据洛伦兹力提供向心力可得：$qvB=m\dfrac{v^{2}}{r}$

联立解得：$U= \dfrac{2qB_{1}^{2}R^{2}}{m}=\dfrac{2qB_{1}^{2}R^{2}}{m}$

若粒子有进入半圆形区域内磁场，求这个区域内磁场的磁感应强度$B_{2}$；

若粒子有进入半圆形区域内磁场，这个区域内磁场的磁感应强度$B_{2}$为$\\dfrac{9}{16}B_{1}$

粒子有进入半圆形区域内磁场时，其运动的轨迹如下图所示：

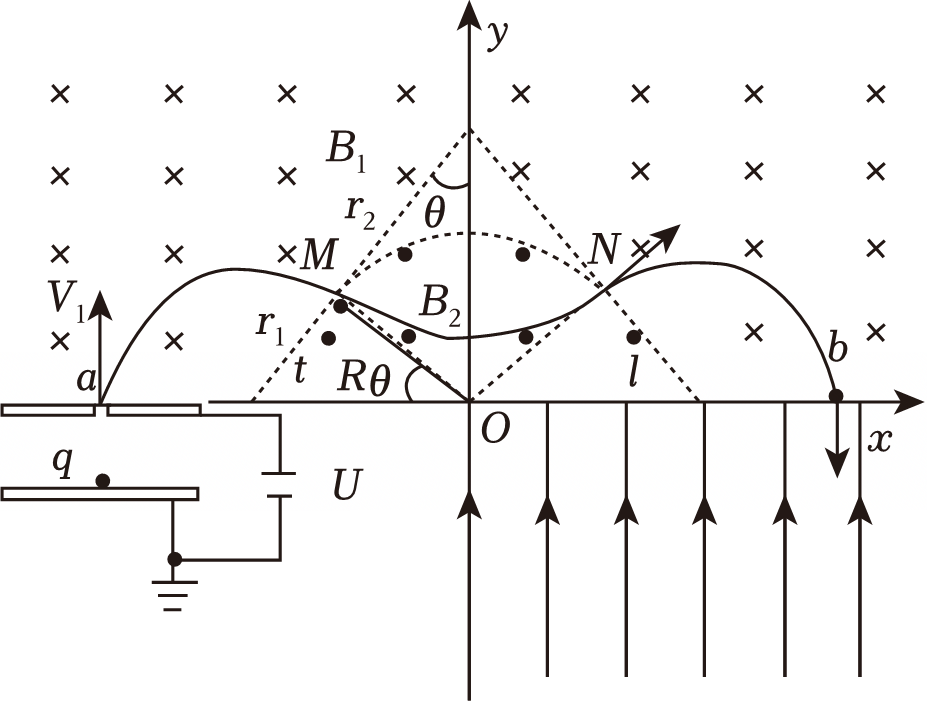
设粒子在磁场$B_{1}$的运动半径为$r_{1}$，则由几何关系可得：$2R=r_{1}+ \sqrt{R^{2}+r_{1}^{2}}$

解得：$r_{1}= \dfrac{3}{4}R$

则有：$\tan\theta= \dfrac{r_{1}}{R}=\dfrac{3}{4}$，可得：$\theta=37^\circ$

粒子在$B_{2}$中的运动半径为：$r_{2}= \dfrac{R}{\tan\theta}=\dfrac{4}{3}R$

根据洛伦兹力提供向心力可得：$qv_{1}B_{1}=m\dfrac{{v_{1}}^{2}}{r_{1}}$；$qv_{1}B_{2}=m\dfrac{{v_{1}}^{2}}{r_{2}}$

可得：$v_{1}= \dfrac{qB_{1}r_{1}}{m}=\dfrac{3kB_{1}R}{4}$

$B_{2}= \dfrac{r_{1}}{r_{2}}B_{1}=\dfrac{9}{16}B_{1}$

在（$2$）问中，从粒子由$a$点飞进磁场开始计时，求粒子以后到达$x$轴的时间。

粒子以后到达$x$轴的时间为$\\dfrac{347\\pi}{162kB_{1}} +n\\left(\\dfrac{3B_{1}R}{2E}+\\dfrac{\\pi}{kB_{1}}\\right)(n=0,1,2,3……)$，和$\\dfrac{347\\pi}{162kB_{1}} k\\left(\\dfrac{3B_{1}R}{2E}+\\dfrac{\\pi}{kB_{1}}\\right)+ \\dfrac{3B_{1}R}{2E}(k=0,1,2,3……)$

粒子在磁场$B_{1}$的运动周期为$T_{1}= \dfrac{2\pi r_{1}}{v_{1}}=\dfrac{2\pi m}{qB_{1}}=\dfrac{2\pi}{kB_{1}}$

粒子由$a$点到$M$点和$N$点到$b$点的轨迹圆心角相等，均为$180^\circ-(90^\circ-37^\circ)=127^\circ$

粒子在磁场$B_{1}$的运动时间为$t_{1}= 2 \times \dfrac{127{^\circ}}{360{^\circ}}T_{1}=\dfrac{127\pi}{90kB_{1}}$

同理，粒子在磁场$B_{2}$的运动周期为$T_{2}= \dfrac{2\pi}{kB_{2}}=\dfrac{32\pi}{9kB_{1}}$

粒子由$M$点到$N$点的轨迹圆心角为$2\theta=2\times 37^\circ=74^\circ$

粒子在磁场$B_{2}$的运动时间为$t_{2}= \dfrac{74{^\circ}}{360{^\circ}}T_{2}=\dfrac{296\pi}{405kB_{1}}$

粒子经$b$点进入第四象限的电场先做匀加速直线运动到速度为零后，再反向做匀加速直线运动到$b$点，设此过程的加速度为$a$，时间为$t_{3}$，则有：$a= \dfrac{qE}{m}=kE$

由对称性可得：$t_{3}= \dfrac{2v_{1}}{a}=\dfrac{3B_{1}R}{2E}$

粒子由$b$点回到第一象限的磁场$B_{1}$，再做顺时针的半个圆周的匀速圆周运动经过$x$轴进入第四象限，此过程的时间为：$t_{4}= \dfrac{1}{2}T_{1}=\dfrac{\pi}{kB_{1}}$

此后粒子在电磁场中做周期性运动，反复经过$x$轴，粒子达到$x$轴的时间为：

当粒子沿$-y$方向经过$x$轴时，所求时间为：$t_{1}+t_{2}+n(t_{3}+t_{4})= \dfrac{347\pi}{162kB_{1}} +n\left(\dfrac{3B_{1}R}{2E}+\dfrac{\pi}{kB_{1}}\right)(n=0,1,2,3……)$

当粒子沿$+y$方向经过$x$轴时，所求时间为：$t_{1}+t_{2}+k(t_{3}+t_{4})+t_{3}= \dfrac{347\pi}{162kB_{1}} +k\left(\dfrac{3B_{1}R}{2E}+\dfrac{\pi}{kB_{1}}\right)+ \dfrac{3B_{1}R}{2E}(k=0,1,2,3……)$。