高中 | 洛伦兹力 题目答案及解析
稿件来源:高途
高中 | 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
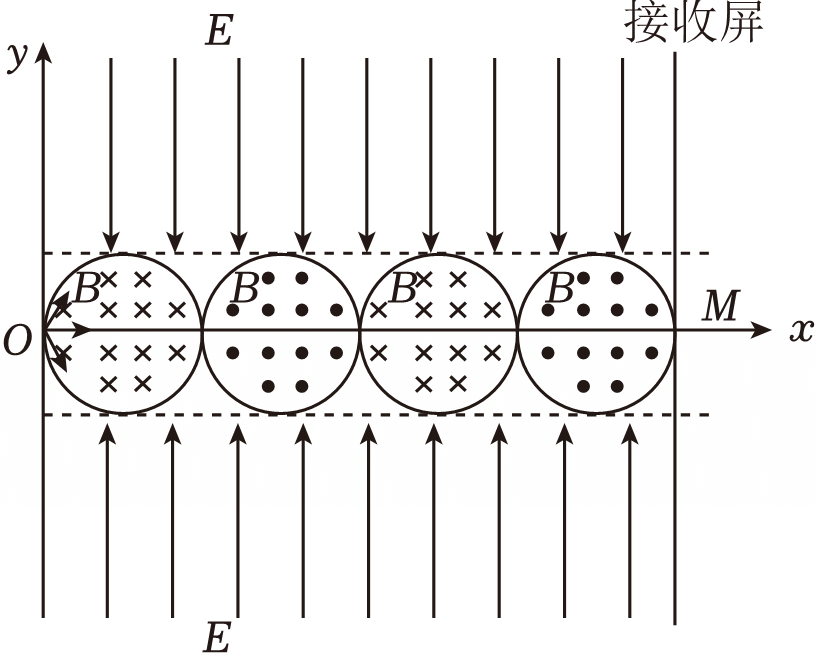
如图所示,真空室中$y$轴右侧存在连续排列的$4$个圆形边界磁场,圆心均在$x$轴上,相邻两个圆相切,半径均为$R$,磁感应强度均为$B$。其中第$1$、$3$个圆形边界的磁场方向垂直于纸面向里,第$2$、$4$个圆形边界的磁场方向垂直于纸面向外,第$4$个磁场右侧有一个粒子接收屏与$x$轴垂直,并与第$4$个磁场相切,切点为$M$,在磁场上方和下方分别有一条虚线与磁场相切,上方虚线以上有一向下的范围无限大的匀强电场,下方虚线以下有一向上的范围无限大的匀强电场,电场强度大小均为$E$。现将一群质量均为$m$、电荷量均为$+q(q\gt 0)$的带电粒子从坐标原点$O$向第一、四象限各个方向发射(不考虑平行于$y$轴方向发射的粒子),射出速度大小均为$v=\dfrac{qBR}{m}$,不计粒子重力,则下列说法正确的是$(\qquad)$
所有粒子从$O$点射出到最终被接收屏接收的过程中在电场中运动的时间均为$\\dfrac{4mv}{qE}$
","所有粒子从$O$点射出到最终被接收屏接收的过程中在磁场中运动的时间均为$\\dfrac{4\\pi m}{qB}$
","所有粒子从$O$点射出到最终被接收屏接收的时间不相同
","所有被接收屏接收的粒子均从$M$点沿$x$轴正方向射出
"]$\rm AD$.粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力有$qvB=m\dfrac{v^{2}}{r}$
解得$r=\dfrac{mv}{qB}=R$
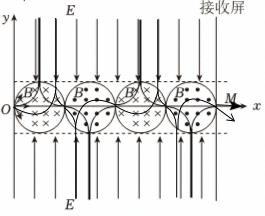
可知粒子的运动满足磁聚焦与磁发散的条件,粒子每次出磁场时速度与$y$轴平行,或会聚于磁场边界与$x$轴的交点,粒子在电场中做匀变速直线运动,且最终会聚与$M$点离开磁场打在接收屏上,其轨迹如图所示
根据牛顿第二定律得$a=\dfrac{qE}{m}$
粒子在电场中运动的时间$t_{1}=4 \times \dfrac{2v}{a}=\dfrac{8mv}{qE}$,故$\rm AD$错误;
$\rm B$.粒子在磁场中运动的周期$T=\dfrac{2\pi m}{qB}$
粒子在磁场中运动时,在每个圆形磁场中轨迹的圆心角都为$180^\circ$,故粒子在磁场中运动的总时间为$t_{2}=4 \times \dfrac{T}{2}=\dfrac{4\pi m}{qB}$,故$\rm B$正确;
$\rm C$.根据前面的分析可知,所以粒子在电场、磁场中运动的总时间都相同,但是在真空无电磁场的区域的运动路程不同,时间不同,所以从$O$点射出到最终被接收屏接收的时间不相同,故$\rm C$正确。
故选:$\rm BC$。
高中 | 洛伦兹力题目答案及解析(完整版)
